
 △ABC为等边三角形,G,H分别从C,A出发,以等速沿CA,AB运动,连CH,BG交于F.
△ABC为等边三角形,G,H分别从C,A出发,以等速沿CA,AB运动,连CH,BG交于F.分析 (1)利用△ABC为等边三角形,G,H分别从C,A出发,以等速沿CA,AB运动,证明△CBH≌△GBA(SAS),得到∠HCB=∠GBA,再利用对顶角相等证明∠HCB=∠HBF,根据∠BFH=∠HCB+∠CBF,即可解答;
(2)(2)如图,在FG上取一点E使BE=BF,连接CE,证明△CFE为等边三角形,利用等边三角形的性质即可得到CB⊥FG.
解答 解:(1)∵G,H分别从C,A出发,以等速沿CA,AB运动,
∴CG=AH,
∵△ABC为等边三角形,
∴AC=AB,∠ABC=∠BAC=60°,
∴CG-AC=AH-AB,即AG=BH,
∠CBH=180°-∠ABC=120°,∠BAG=180°-∠BAC=120°,
∴∠CBH=∠BAG,
在△CBH和△GBA中,
$\left\{\begin{array}{l}{BH=AG}\\{∠CBH=∠GAB}\\{CB=BA}\end{array}\right.$
∴△CBH≌△GBA(SAS),
∴∠HCB=∠GBA,
∵∠GBA=∠HBF,
∴∠HCB=∠HBF,
∵∠BFH=∠HCB+∠CBF,
∴∠BFH=∠HBF+∠CBF=∠CBH=120°.
(2)如图,在FG上取一点E使BE=BF,连接CE,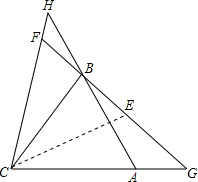
∵∠BFH=120°,
∴∠BFC=60°,
∵CF=2BF,BF=BE,
∴FC=FE,
∴△CFE为等边三角形,
∵B为EF的中点,
∴CB⊥EF,
∵F,B,G,E在同一条直线上,
∴CB⊥FG.
点评 本题考查了全等三角形的性质定理与判定定理、等边三角形的性质,解决本题的关键是作出辅助线,构建全等三角形.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,⊙O半径为4cm,其内接正六边形ABCDEF,点P,Q同时分别从A,D两点出发,以1cm/s速度沿AF,DC向中点F,G运动.连接PB,QE,设运动时间为t(s).
如图,⊙O半径为4cm,其内接正六边形ABCDEF,点P,Q同时分别从A,D两点出发,以1cm/s速度沿AF,DC向中点F,G运动.连接PB,QE,设运动时间为t(s).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
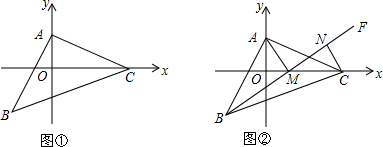
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com