
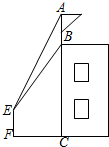
 如图,某建筑物BC上有一旗杆AB,小明在F处,由E点观察到旗杆顶部A的仰角为52°,底部B的仰角为45°,小明的观测点与地面距离EF为1.6m,
如图,某建筑物BC上有一旗杆AB,小明在F处,由E点观察到旗杆顶部A的仰角为52°,底部B的仰角为45°,小明的观测点与地面距离EF为1.6m,分析 (1)先过点E作ED⊥BC于D,由已知底部B的仰角为45°得BD=ED=FC=12,DC=EF=1.6,从而求出BC.
(2)在Rt△ADB中,根据正切函数得出$\frac{AB+BD}{BD}$=$\frac{3.15+BD}{BD}$=1.28,从而求得BD,进而求得BC=BD+DC=12.9.
解答  解:(1)过点E作ED⊥BC于D,根据题意得:EF⊥FC,ED∥FC,
解:(1)过点E作ED⊥BC于D,根据题意得:EF⊥FC,ED∥FC,
∴四边形CDEF是矩形,
已知底部B的仰角为45°即∠BED=45°,
∴∠EBD=45°,
∴BD=ED=FC=12,
∴BC=BD+DC=BD+EF=12+1.6=13.6,
答:建筑物BC的高度为13.6m.
(2)在Rt△ADB中,∠ADB=90°,∠AED=52°
∴tan∠AED=$\frac{AD}{ED}=\frac{AB+BD}{ED}=\frac{3.15+BD}{BD}=1.28$
∴BD=11.25
∴BC=11.25+1.6=12.85≈12.9m.
点评 此题考查的知识点是解直角三角形的应用,解题的关键是把实际问题转化为解直角三角形问题,先得到等腰直角三角形,再根据三角函数求解.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:解答题
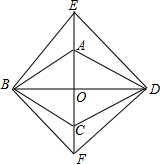 如图,菱形ABCD的对角线AC,BD相交于点O,分别延长OA,OC到点E,F,使AE=CF,依次连接B,F,D,E各点.
如图,菱形ABCD的对角线AC,BD相交于点O,分别延长OA,OC到点E,F,使AE=CF,依次连接B,F,D,E各点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,AB=AC=20,cosC=$\frac{\sqrt{5}}{5}$.
如图,△ABC中,AB=AC=20,cosC=$\frac{\sqrt{5}}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点O在∠APB的平分线上,⊙O与PA相切于点C.
如图,点O在∠APB的平分线上,⊙O与PA相切于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
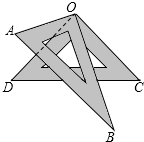 如图,将一幅三角尺叠放在一起,使直角顶点重合于点O,绕点O任意转动其中一个三角尺,则与∠AOD始终相等的角是( )
如图,将一幅三角尺叠放在一起,使直角顶点重合于点O,绕点O任意转动其中一个三角尺,则与∠AOD始终相等的角是( )| A. | ∠BOD | B. | ∠ABO | C. | ∠BOC | D. | ∠BAO |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com