
【题目】如图,以直角三角形AOC的直角顶点O为原点,以OC、OA所在直线为x轴和y轴建立平面直角坐标系,点![]() ,
,![]() 满足
满足![]() .
.
![]() 则C点的坐标为______;A点的坐标为______.
则C点的坐标为______;A点的坐标为______.
![]() 已知坐标轴上有两动点P、Q同时出发,P点从C点出发沿x轴负方向以1个单位长度每秒的速度匀速移动,Q点从O点出发以2个单位长度每秒的速度沿y轴正方向移动,点Q到达A点整个运动随之结束
已知坐标轴上有两动点P、Q同时出发,P点从C点出发沿x轴负方向以1个单位长度每秒的速度匀速移动,Q点从O点出发以2个单位长度每秒的速度沿y轴正方向移动,点Q到达A点整个运动随之结束![]() 的中点D的坐标是
的中点D的坐标是![]() ,设运动时间为
,设运动时间为![]() 秒
秒![]() 问:是否存在这样的t,使
问:是否存在这样的t,使![]() ?若存在,请求出t的值;若不存在,请说明理由.
?若存在,请求出t的值;若不存在,请说明理由.
![]() 点F是线段AC上一点,满足
点F是线段AC上一点,满足![]() ,点G是第二象限中一点,连OG,使得
,点G是第二象限中一点,连OG,使得![]() 点E是线段OA上一动点,连CE交OF于点H,当点E在线段OA上运动的过程中,
点E是线段OA上一动点,连CE交OF于点H,当点E在线段OA上运动的过程中,![]() 的值是否会发生变化?若不变,请求出它的值;若变化,请说明理由.
的值是否会发生变化?若不变,请求出它的值;若变化,请说明理由.

【答案】(1)![]() ;
;![]() ;(2)1;(3)2.
;(2)1;(3)2.
【解析】
(1)根据绝对值和算术平方根的非负性,求得a,b的值即可;
(2)先得出CP=t,OP=2﹣t,OQ=2t,AQ=4﹣2t,再根据S△ODP=S△ODQ,列出关于t的方程,求得t的值即可;
(3)过H点作AC的平行线,交x轴于P,先判定OG∥AC,再根据角的和差关系以及平行线的性质,得出∠PHO=∠GOF=∠1+∠2,∠OHC=∠OHP+∠PHC=∠GOF+∠4=∠1+∠2+∠4,最后代入![]() 进行计算即可.
进行计算即可.
(1)∵![]() +|b﹣2|=0,∴a﹣2b=0,b﹣2=0,解得:a=4,b=2,∴A(0,4),C(2,0);
+|b﹣2|=0,∴a﹣2b=0,b﹣2=0,解得:a=4,b=2,∴A(0,4),C(2,0);
(2)由条件可知:P点从C点运动到O点时间为2秒,Q点从O点运动到A点时间为2秒,∴0<t≤2时,点Q在线段AO上,即 CP=t,OP=2﹣t,OQ=2t,AQ=4﹣2t,∴ .
.
∵S△ODP=S△ODQ,∴2﹣t=t,∴t=1;
(3)![]() 的值不变,其值为2.
的值不变,其值为2.
∵∠2+∠3=90°.
又∵∠1=∠2,∠3=∠FCO,∴∠GOC+∠ACO=180°,∴OG∥AC,∴∠1=∠CAO,∴∠OEC=∠CAO+∠4=∠1+∠4,如图,过H点作AC的平行线,交x轴于P,则∠4=∠PHC,PH∥OG,∴∠PHO=∠GOF=∠1+∠2,∴∠OHC=∠OHP+∠PHC=∠GOF+∠4=∠1+∠2+∠4,∴![]() .
.



 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:
【题目】已知,∠AOB=90°,点C在射线OA上,CD∥OE.
(1)如图1,若∠OCD=120°,求∠BOE的度数;
(2)把“∠AOB=90°”改为“∠AOB=120°”,射线OE沿射线OB平移,得O′E,其他条件不变,(如图2所示),探究∠OCD、∠BO′E的数量关系;
(3)在(2)的条件下,作PO′⊥OB垂足为O′,与∠OCD的平分线CP交于点P,若∠BO′E=α,请用含α的式子表示∠CPO′(请直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】早晨,小明步行到离家900米的学校去上学,到学校时发现眼镜忘在家中,于是他立即按原路步行回家,拿到眼镜后立即按原路骑自行车返回学校.已知小明步行从学校到家所用的时间比他骑自行车从家到学校所用的时间多10分钟,小明骑自行车速度是步行速度的3倍.
(1)求小明步行速度(单位:米/分)是多少;
(2)下午放学后,小明骑自行车回到家,然后步行去图书馆,如果小明骑自行车和步行的速度不变,小明步行从家到图书馆的时间不超过骑自行车从学校到家时间的2倍,那么小明家与图书馆之间的路程最多是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两同学同时从山脚开始爬山,到达山顶后立即下山,在山脚和山顶之间不断往返运动,已知山坡长为360m,甲、乙上山的速度比是6:4,并且甲、乙下山的速度都是各自上山速度的1.5倍,当甲第三次到达山顶时,则此时乙所在的位置是![]() 。
。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的5个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:
(1)这次调查的学生共有多少名?
(2)请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数.
(3)如果要在这5个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,∠ABD和∠BDC的平分线相交于点E,BE交CD于点F, ∠1+∠2=90°.

(1)AB与CD平行吗?试说明理由.
(2)试探究∠2与∠3的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长均为1个单位的正方形网格图中,建立了平面直角坐标系xOy,按要求解答下列问题:

(1)写出△ABC三个顶点的坐标;
(2)画出△ABC向右平移6个单位后得到的图形△A1B1C1;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2﹣2ax﹣3a(a<0)与x轴交于A,B两点,点A在点B的左边,与y轴交于点C,顶点为D,若以BD为直径的⊙M经过点C.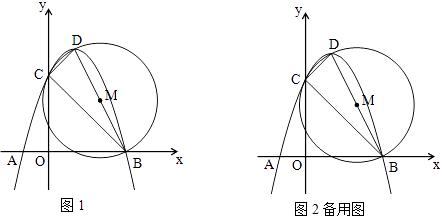
(1)请直接写出C,D两点的坐标(用含a的代数式表示);
(2)求抛物线的函数表达式;
(3)在抛物线上是否存在点E,使∠EDB=∠CBD?若存在,请求出所有满足条件的点E的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com