

分析 (1)由平行四边形、矩形、菱形、正方形的性质和“完美筝形”的定义容易得出结论;
(2)先证出∠AEB′=∠BCB′,再求出∠BCE=∠ECF=40°,即可得出结果;
(3)由折叠的性质得出BE=B′E,BC=B′C,∠B=∠CB′E=90°,CD=CD′,FD=FD′,∠D=∠CD′F=90°,即可得出四边形EBCB′、四边形FDCD′是“完美筝形”;
由题意得出∠OD′E=∠OB′F=90°,CD′=CB′,由菱形的性质得出AE=AF,CE=CF,再证明△OED′≌△OFB′,得出OD′=OB′,OE=OF,证出∠AEB′=∠AFD′=90°,即可得出四边形CD′OB′、四边形AEOF是“完美筝形”;即可得出结论;
当图③中的∠BCD=90°时,四边形ABCD是正方形,证明A、E、B′、F四点共圆,得出$\widehat{AE}=\widehat{AF}$,由圆周角定理即可得出∠AB′E的度数.
解答 解:(1)①∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,∠A=∠C≠90°,∠B=∠D≠90°,
∴AB≠AD,BC≠CD,
∴平行四边形不一定为“完美筝形”;
②∵四边形ABCD是矩形,
∴∠A=∠B=∠C=∠D=90°,AB=CD,AD=BC,
∴AB≠AD,BC≠CD,
∴矩形不一定为“完美筝形”;
③∵四边形ABCD是菱形,
∴AB=BC=CD=AD,∠A=∠C≠90°,∠B=∠D≠90°,
∴菱形不一定为“完美筝形”;
④∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=AD,
∴正方形一定为“完美筝形”;
∴在平行四边形、矩形、菱形、正方形四种图形中,一定为“完美筝形”的是正方形;
故答案为:正方形;
(2)根据题意得:∠B′=∠B=90°,
∴在四边形CBEB′中,∠BEB′+∠BCB′=180°,
∵∠AEB′+∠BEB′=180°,
∴∠AEB′=∠BCB′,
∵∠BCE=∠ECF=∠FCD,∠BCD=120°,
∴∠BCE=∠ECF=40°,
∴∠AEB′=∠BCB′=40°+40°=80°;
故答案为:80;
(3)当图②中的四边形AECF为菱形时,对应图③中的“完美筝形”有5个;理由如下;
根据题意得:BE=B′E,BC=B′C,∠B=∠CB′E=90°,CD=CD′,FD=FD′,∠D=∠CD′F=90°,
∴四边形EBCB′、四边形FDCD′是“完美筝形”;
∵四边形ABCD是“完美筝形”,
∴AB=AD,CB=CD,∠B=∠D=90°,
∴CD′=CB′,∠CD′O=∠CB′O=90°,
∴∠OD′E=∠OB′F=90°,
∵四边形AECF为菱形,
∴AE=AF,CE=CF,AE∥CF,AF∥CE,
∴D′E=B′F,∠AEB′=∠CB′E=90°,∠AFD′=∠CD′F=90°,
在△OED′和△OFB′中,$\left\{\begin{array}{l}{∠OD′E=∠OB′F}&{\;}\\{∠EOD′=∠FOB′}&{\;}\\{D′E=B′F}&{\;}\end{array}\right.$,
∴△OED′≌△OFB′(AAS),
∴OD′=OB′,OE=OF,
∴四边形CD′OB′、四边形AEOF是“完美筝形”;
∴包含四边形ABCD,对应图③中的“完美筝形”有5个;
故答案为:5;
当图③中的∠BCD=90°时,如图所示: 四边形ABCD是正方形,
四边形ABCD是正方形,
∴∠BAD=90°,
∵∠EB′F=90°,
∴∠BAD+∠EB′F=180°,
∴A、E、B′、F四点共圆,
∵AE=AF,
∴$\widehat{AE}=\widehat{AF}$,
∴∠AB′E=∠AB′F=$\frac{1}{2}$∠EB′F=45°.
点评 本题是四边形综合题目,考查了平行四边形、矩形、菱形、正方形的性质、“完美筝形”的判定与性质、全等三角形的判定与性质、四点共圆、圆周角定理等知识;本题难度较大,综合性强,熟练掌握“完美筝形”的定义,并能进行推理论证与计算是解决问题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
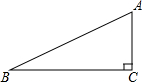 如图,在△ABC中,∠ACB=90°,∠ABC=26°,BC=5.若用科学计算器求边AC的长,则下列按键顺序正确的是( )
如图,在△ABC中,∠ACB=90°,∠ABC=26°,BC=5.若用科学计算器求边AC的长,则下列按键顺序正确的是( )| A. | 5÷tan26°= | B. | 5÷sin26°= | C. | 5×cos26°= | D. | 5×tan26°= |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
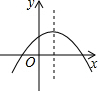 二次函数y=ax2+bx+c的图象在平面直角坐标系中的位置如图所示,则一次函数y=ax+b与反比例函数y=$\frac{c}{x}$在同一平面直角坐标系中的图象可能是( )
二次函数y=ax2+bx+c的图象在平面直角坐标系中的位置如图所示,则一次函数y=ax+b与反比例函数y=$\frac{c}{x}$在同一平面直角坐标系中的图象可能是( )| A. | 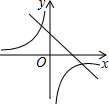 | B. |  | C. | 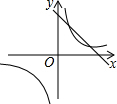 | D. | 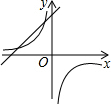 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
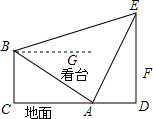 如图所示,体育场内一看台与地面所成夹角为30°,看台最低点A到最高点B的距离为10$\sqrt{3}$,A,B两点正前方有垂直于地面的旗杆DE.在A,B两点处用仪器测量旗杆顶端E的仰角分别为60°和15°(仰角即视线与水平线的夹角)
如图所示,体育场内一看台与地面所成夹角为30°,看台最低点A到最高点B的距离为10$\sqrt{3}$,A,B两点正前方有垂直于地面的旗杆DE.在A,B两点处用仪器测量旗杆顶端E的仰角分别为60°和15°(仰角即视线与水平线的夹角)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com