
【题目】综合与探究
数学课上,老师让同学们利用三角形纸片进行操作活动,探究有关线段之间的关系.
问题情境:
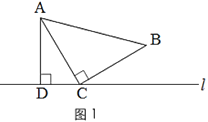
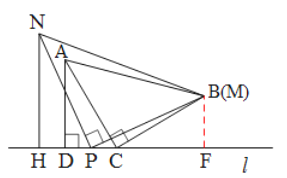
如图1,三角形纸片ABC中,∠ACB=90°,AC=BC.将点C放在直线l上,点A,B位于直线l的同侧,过点A作AD⊥l于点D.
初步探究:
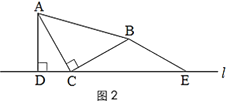
(1)在图1的直线l上取点E,使BE=BC,得到图2.猜想线段CE与AD的数量关系,并说明理由;
变式拓展:
(2)小颖又拿了一张三角形纸片MPN继续进行拼图操作,其中∠MPN=90°,MP=NP.小颖在图 1 的基础上,将三角形纸片MPN的顶点P放在直线l上,点M与点B重合,过点N作NH⊥l于点 H.
请从下面 A,B 两题中任选一题作答,我选择_____题.
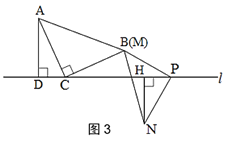
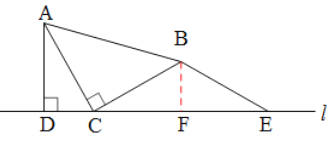
A.如图3,当点N与点M在直线l的异侧时,探究此时线段CP,AD,NH之间的数量关系,并说明理由.
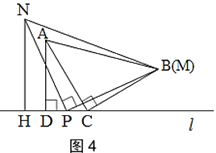
B.如图4,当点N与点M在直线l的同侧,且点P在线段CD的中点时,探究此时线段CD,AD,NH之间的数量关系,并说明理由.
【答案】(1)CE=2AD;(2)A题:CP=AD+NH;B题:NH=![]() CD+AD.
CD+AD.
【解析】
(1) 过点B作BF⊥l于点F,通过已知条件证得△ACD≌△CBF,再通过等腰三角形性质即可求解.
(2) ①过点B作BF⊥l于点F,通过已知条件△ACD≌△CBF证得△BFP≌△PHN,即可得出边边之间关系.
②过点B作BF⊥l于点F,通过已知条件△ACD≌△CBF证得△BFP≌△PHN,再通过边边转化即可求解.
(1)CE=2AD,理由如下:
过点B作BF⊥l于点F,易得∠CFB=90°
∵AD⊥l
∴∠ADC=90°,∠CAD+∠DCA=90°
∴∠ADC=∠CFB
∵∠ACB=90°
∴∠DCA+∠BCF=90°
∴∠CAD=∠BCF
在△ACD和△CBF 中
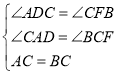
∴△ACD≌△CBF(AAS)
∴AD=CF
∵BE=BC,BF⊥l
∴CF=EF
∴CE=2CF=2AD
(2)A.CP=AD+NH,理由如下:
过点B作BF⊥l于点F,易得∠BFP=90°,
由(1)可得:△ACD≌△CBF
∴AD=CF
∵NH⊥l
∴∠PHN=90°,∠HNP+∠HPN=90°
∴∠BFP=∠PHN
∵∠MPN=90°
∴∠HPN+∠FPB=90°
∴∠HNP=∠FPB
在△BFP和△PHN 中
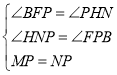
∴△BFP≌△PHN(AAS)
∴NH=PF
∵CP=CF+PF
∴CP=AD+NH
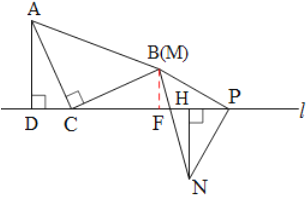
B.NH=![]() CD+AD,理由如下:
CD+AD,理由如下:
过点B作BF⊥l于点F,易得∠BFC=90°,
由(1)可得:△ACD≌△CBF
∴AD=CF
∵NH⊥l
∴∠PHN=90°,∠HNP+∠HPN=90°
∴∠BFP=∠PHN
∵∠MPN=90°
∴∠HPN+∠FPB=90°
∴∠HNP=∠FPB
在△BFP 和△PHN中
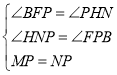
∴△BFP≌△PHN(AAS)
∴NH=PF
∵点P在线段CD的中点
∴CP=DP=![]() CD
CD
由图得:PF=PC+CF
∴NH=![]() CD+AD
CD+AD


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案科目:初中数学 来源: 题型:
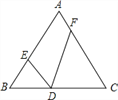
【题目】如图,在等边△ABC中,边长为6,D是BC边上的动点,∠EDF=60°.
(1)求证:△BDE∽△CFD;
(2)当BD=1,CF=3时,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设中学生体质健康综合评定成绩为![]() 分,满分为100分,规定:
分,满分为100分,规定:![]() 为
为![]() 级,
级,![]() 为
为![]() 级,
级,![]() 为
为![]() 级,
级,![]() 为
为![]() 级.现随机抽取某中学部分学生的综合评定成绩,整理绘制成如下两幅不完整的统计图,请根据图中的信息,解答下列问题:
级.现随机抽取某中学部分学生的综合评定成绩,整理绘制成如下两幅不完整的统计图,请根据图中的信息,解答下列问题:

(1)在这次调查中,一共抽取了__________名学生;
(2)扇形统计图中,![]() ________%,
________%,![]() 级对应的圆心角为______度;
级对应的圆心角为______度;
(3)若该中学共有学生1200名,请你利用你所学的统计知识,估计综合评定成绩为![]() 级的学生有多少名?
级的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的图象的顶点为A.二次函数
的图象的顶点为A.二次函数![]() 的图象与x轴交于原点O及另一点C,它的顶点B在函数
的图象与x轴交于原点O及另一点C,它的顶点B在函数![]() 的图象的对称轴上.
的图象的对称轴上.
(1)求点A与点C的坐标;
(2)当四边形AOBC为菱形时,求函数![]() 的关系式.
的关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
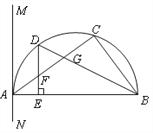
【题目】如图,△ABC内接于半圆,AB是直径,过A作直线MN,若∠MAC=∠ABC.
(1)求证:MN是半圆的切线;
(2)设D是弧AC的中点,连结BD交AC 于G,过D作DE⊥AB于E,交AC于F.求证:FD=FG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个用来盛爆米花的圆锥形纸杯,纸杯开口的直径 EF 长为10cm,母线OE(OF)长为10cm,在母线OF 上的点A 处有一块爆米花残渣且FA=2cm,一只蚂蚁从杯口的点E 处沿圆锥表面爬行到A 点,则此蚂蚁爬行的最短距离为 cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园手机”现象越来越受到社会的关注.“五一”期间,小记者刘铭随机调查了城区若干名学生和家长对中学生带手机现象的看法,统计整理并制作了如下的统计图:

(1)求这次调查的家长人数,并补全图①;
(2)求图②中表示家长“赞成”的圆心角的度数;
(3)如果该市有8万名初中生,持“无所谓”态度的学生大约有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com