

A、
| ||
B、
| ||
C、
| ||
D、
|
科目:初中数学 来源: 题型:
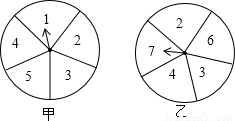
 在如图的甲、乙两个转盘中,指针指向每一个数字的机会是均等的.
在如图的甲、乙两个转盘中,指针指向每一个数字的机会是均等的.查看答案和解析>>
科目:初中数学 来源: 题型:
 在如图的甲、乙两个转盘中,指针指向每一个数字的机会是均等的.当同时转动两个转盘,停止后指针所指的两个数字表示两条线段的长,如果第三条线段的长为5,那么这三条线段能构成三角形的概率为
在如图的甲、乙两个转盘中,指针指向每一个数字的机会是均等的.当同时转动两个转盘,停止后指针所指的两个数字表示两条线段的长,如果第三条线段的长为5,那么这三条线段能构成三角形的概率为查看答案和解析>>
科目:初中数学 来源:2011年南京市六合区中考数学一模试卷 题型:填空题
在如图的甲、乙两个转盘中,指针指向每一个数字的机会是均等的.当同时转动两个转盘,停止后指针所指的两个数字表示两条线段的长,如果第三条线段的长为5,那么这三条线段能构成三角形的概率为_____________.

查看答案和解析>>
科目:初中数学 来源:第33章《概率的计算和估计》中考题集(01):33.1 用列举法求概率(解析版) 题型:选择题
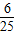

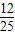
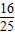
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com