
【题目】阅读下列材料解决问题
两个多位数整数,若它们各数位上的数字之和相等,则称这两个多位数互为“调和数”,例如37和82,它们各数位上的数字之和分别为3+7和8+2,显然3+7=8+2=10故37和82互为“调和数”.
(1)下列说法错误的是
A.123和51互为调和数” B.345和513互为“调和数
C.2018和8120互为“调和数” D.两位数![]() 和
和![]() 互为“调和数”
互为“调和数”
(2)若A、B是两个不等的两位数,A=![]() ,B=
,B=![]() ,A和B互为“调和数”,且A与B之和是B与A之差的3倍,求满足条件的两位数A.
,A和B互为“调和数”,且A与B之和是B与A之差的3倍,求满足条件的两位数A.
【答案】(1)B(2)18
【解析】
(1)根据题意,两个多位数整数,若它们各数位上的数字之和相等,则称这两个多位数互为“调和数”,即可作答
(2)先用“调和数”,得出x+y=m+n,再利用A与B之和是B与A之差的3倍,得出10m+n=20x+2y,即可得出m=![]() ,最后利用1≤x≤9,0≤y≤9,计论即可以得出结论
,最后利用1≤x≤9,0≤y≤9,计论即可以得出结论
(1)根据调和数的定义,通过计算各位数之和,易知B选项错误
故答案选B
(2)∵A=![]() ,B=
,B=![]() ,A、B互为“调和数”
,A、B互为“调和数”
∴x+y=m+n①
∵A与B之和是B与A之差的3倍
∴![]()
∴![]()
∴10m+n=20x+2y②
由①②得,m=![]()
∵m为两位数的十位数字
∴1≤m≤9
∴1≤![]() ≤9,
≤9,
∴9≤19x+y≤81,且19x+y是9的倍数
∴19x+y=18或27或36或45或54或63或72或81
则![]() 或
或![]() 或
或![]() 或
或![]() 或
或![]() 或
或![]() 或
或![]() 或
或![]()
∵x,y分别为A的 十位和个位,
∴1≤x≤9,0≤y≤9
∴计算可得,仅当![]() 时满足,此时x=1,y=8,故A为18
时满足,此时x=1,y=8,故A为18
故满足A的值为18


科目:初中数学 来源: 题型:
【题目】(14分)盘锦红海滩景区门票价格80元/人,景区为吸引游客,对门票价格进行动态管理,非节假日打a折,节假日期间,10人以下(包括10人)不打折,10人以上超过10人的部分打b折,设游客为x人,门票费用为y元,非节假日门票费用![]() (元)及节假日门票费用
(元)及节假日门票费用![]() (元)与游客x(人)之间的函数关系如图所示.
(元)与游客x(人)之间的函数关系如图所示.

(1)a= ,b= ;
(2)直接写出![]() 、
、![]() 与x之间的函数关系式;
与x之间的函数关系式;
(3)导游小王6月10日(非节假日)带A旅游团,6月20日(端午节)带B旅游团到红海滩景区旅游,两团共计50人,两次共付门票费用3040元,求A、B两个旅游团各多少人?
【答案】(1)6,8;(2)![]() ,
,![]() =
=![]() ;(3)A团有20人,B团有30人.
;(3)A团有20人,B团有30人.
【解析】
试题(1)由函数图象,用购票款数除以定价的款数,得出a的值;用第11人到20人的购票款数除以定价的款数,得出b的值;
(2)利用待定系数法求正比例函数解析式求出![]() ,分x≤10与x>10,利用待定系数法求一次函数解析式求出
,分x≤10与x>10,利用待定系数法求一次函数解析式求出![]() 与x的函数关系式即可;
与x的函数关系式即可;
(3)设A团有n人,表示出B团的人数为(50﹣n),然后分0≤n≤10与n>10两种情况,根据(2)的函数关系式列出方程求解即可.
试题解析:(1)由![]() 图象上点(10,480),得到10人的费用为480元,∴a=
图象上点(10,480),得到10人的费用为480元,∴a=![]() ×10=6;
×10=6;
由y2图象上点(10,800)和(20,1440),得到20人中后10人费用为640元,∴b=![]() ×10=8;
×10=8;
(2)设![]() ,∵函数图象经过点(0,0)和(10,480),∴
,∵函数图象经过点(0,0)和(10,480),∴![]() ,∴
,∴![]() =48,∴
=48,∴![]() ;
;
0≤x≤10时,设![]() ,∵函数图象经过点(0,0)和(10,800),∴
,∵函数图象经过点(0,0)和(10,800),∴![]() ,∴
,∴![]() =80,∴
=80,∴![]() ,x>10时,设
,x>10时,设![]() ,∵函数图象经过点(10,800)和(20,1440),∴
,∵函数图象经过点(10,800)和(20,1440),∴![]() ,∴
,∴![]() ,∴
,∴![]() ;
;
∴![]() =
=![]() ;
;
(3)设A团有n人,则B团的人数为(50﹣n),当0≤n≤10时,48n+80(50﹣n)=3040,解得n=30(不符合题意舍去),当n>10时,48n+64(50﹣n)+160=3040,解得n=20,则50﹣n=50﹣20=30.
答:A团有20人,B团有30人.
考点:1.一次函数的应用;2.分段函数;3.分类讨论;4.综合题.
【题型】解答题
【结束】
23
【题目】在平面直角坐标系xOy中有一点,过该点分别作x轴和y轴的垂线,垂足分别是A、B,若由该点、原点O以及两个垂足所组成的长方形的周长与面积的数值相等,则我们把该点叫做平面直角坐标系中的平衡点.
![]() 请判断下列各点中是平面直角坐标系中的平衡点的是______;
请判断下列各点中是平面直角坐标系中的平衡点的是______;![]() 填序号
填序号![]()
![]() ,
,![]() .
.
![]() 若在第一象限中有一个平衡点
若在第一象限中有一个平衡点![]() 恰好在一次函数
恰好在一次函数![]() 为常数
为常数![]() 的图象上.
的图象上.
![]() 求m、b的值;
求m、b的值;
![]() 一次函数
一次函数![]() 为常数
为常数![]() 与y轴交于点C,问:在这函数图象上,是否存在点
与y轴交于点C,问:在这函数图象上,是否存在点![]() 使
使![]() ,若存在,请直接写出点M的坐标;若不存在,请说明理由.
,若存在,请直接写出点M的坐标;若不存在,请说明理由.
![]() 经过点
经过点![]() ,且平行于x轴的直线上有平衡点吗?若有,请求出平衡点的坐标;若没有,说明理由.
,且平行于x轴的直线上有平衡点吗?若有,请求出平衡点的坐标;若没有,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在期末考试来临之际,同学们都进入紧张的复习阶段,为了了解同学们晚上的睡眠情况,现对年级部分同学进行了调查统计,并制成如下两幅不完整的统计图:(其中A代表睡眠时间8小时左右,B代表睡眠时间6小时左右,C代表睡眠时间4小时左右,D代表睡眠时间5小时左右,E代表睡眠时间7小时左右),其中扇形统计图中“E”的圆心角为90°,请你结合统计图所给信息解答下列问题:
(1)共抽取了 名同学进行调查,同学们的睡眠时间的中位数是 小时左右,并将条形统计图补充完整;
(2)请你估计年级每个学生的平均睡眠时间约多少小时?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,G是边长为8的正方形ABCD的边BC上的一点,矩形DEFG的边EF过点A,GD=10.
(1)求FG的长;
(2)直接写出图中与△BHG相似的所有三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家禽养殖场,用总长为110m的围栏靠墙(墙长为22m)围成如图所示的三块矩形区域,矩形AEHG与矩形CDEF面积都等于矩形BFHG面积的一半,设AD长为xm,矩形区域ABCD的面积为ym2 . 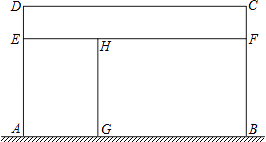
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)当x为何值时,y有最大值?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①abc>0,②a﹣b+c<0,③2a+b=0,④b2﹣4ac>0,其中正确结论个数是( )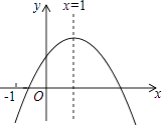
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD.∠1=∠2,∠3=∠4,试说明 AD∥BE,请你将下面解答过程填写完整.

解:∵AB∥CD,
∴∠4= ( )
∵∠3=∠4
∴∠3= (等量代换)
∵∠1=∠2
∴∠1+∠CAF=∠2+∠CAE 即∠BAE= .
∴∠3= ( )
∴AD∥BE( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一个水池,其底面是边长为16尺的正方形,一根芦苇AB生长在它的正中央,高出水面部分BC的长为2尺,如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的B′,则这根芦苇AB的长是( )
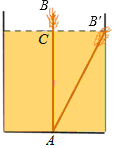
A. 15尺B. 16尺C. 17尺D. 18尺
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com