
填空题
(1)已知 ,
, ,则
,则 .
.
(2)已知 ,则m=________.
,则m=________.
(3)已知 无意义,则x的取值范围是________.
无意义,则x的取值范围是________.
(4)已知 ,则A=_________.
,则A=_________.
(5)若 且
且 ,则mn=________.
,则mn=________.
|
(1) 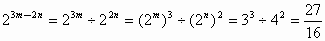 . .
(2)∵ 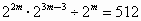 , ,
即 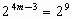
∴4m-3=9.∴m=3. (3)∵ 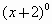 无意义,∴x+2=0,∴x=-2. 无意义,∴x+2=0,∴x=-2.
(4) 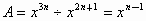 . .
(5)∵ 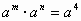 ,∴m+n=4 ,∴m+n=4
∵ 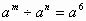 ,∴m-n=6 ,∴m-n=6
∴ 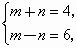
解得 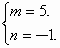
故mn=-5 |
|
本题考查同底数幂的运算公式的灵活应用,有正用的也有逆用的,在第(1)小题中,要算  的值,先逆用同底数幂的除法公式 的值,先逆用同底数幂的除法公式 = = ÷ ÷ 得, 得, ,然后在逆用幂的乘方公式得 ,然后在逆用幂的乘方公式得 ,最后再把已知代入即可得到答案;在第(2)小题中,先化为同底数幂的乘除法,再用公式,后把等式右边的512化成 ,最后再把已知代入即可得到答案;在第(2)小题中,先化为同底数幂的乘除法,再用公式,后把等式右边的512化成 ,就可得到关于m的方程,从而求出m的值;第(3)小题考察零指数幂的条件,底数不为0;第(4)小题看成解关于A的一次方程,此时x是常数;第(5)小题利用同底数幂的乘除法把指数转化成加减法,根据量数和与两数差的值平方后推出两数积的值. ,就可得到关于m的方程,从而求出m的值;第(3)小题考察零指数幂的条件,底数不为0;第(4)小题看成解关于A的一次方程,此时x是常数;第(5)小题利用同底数幂的乘除法把指数转化成加减法,根据量数和与两数差的值平方后推出两数积的值. |


科目:初中数学 来源: 题型:
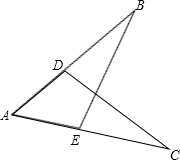 说理题:
说理题:
|
查看答案和解析>>
科目:初中数学 来源: 题型:
 29、附加题
29、附加题查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
 24、阅读填空题:
24、阅读填空题:查看答案和解析>>
科目:初中数学 来源: 题型:
| b |
| a |
| c |
| a |
| b |
| a |
| b |
| a |
| c |
| a |
| c |
| a |
查看答案和解析>>
科目:初中数学 来源: 题型:
| a |
| 4 |
| b |
| 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com