练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    9．已知x-2y=3，则3-2x+4y=-3．

    分析 原式变形后，将已知等式代入计算即可求出值．

    解答 解：当x-2y=3时，原式=3-2（x-2y）=3-6=-3，
    故答案为：-3

    点评 此题考查了代数式求值，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    19．若x、y满足方程组$\left\{\begin{array}{l}{x+2y=5}\\{2x+y=3}\end{array}\right.$，则x-y的值等于（　　）
    A．-1B．1C．-2D．2

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．如图，菱形ABCD的周长为16，若∠BAD=60°，E是AB的中点，则点E的坐标为（$\sqrt{3}$，1）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．若关于x的一元二次方程kx2-6x+9=0有两个相等的实数根，那么k的取值为（　　）
    A．k＞1B．k＜1C．k=1D．k＜1且k≠0

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．计算：$\root{3}{8}$的值是（　　）
    A．8B．±2C．-2D．2

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

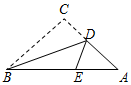    14．如图，三角形纸片ABC，AB=10cm，BC=7cm，AC=6cm，沿过点B的直线折叠这个三角形，使顶点C落在AB边上的点E处，折痕为BD，则△AED的周长为（　　）cm．
    A．9B．13C．16D．10

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．两位老师准备组织七年级（1）班的学生去宜兴竹海春游，甲、乙两家旅行杜的报价相同，且都表示还可提供优惠，其中，甲旅行社对老师和学生一律7折收费，乙旅行社对老师免费，学生8折收费，请问他们应选择哪家旅行社？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

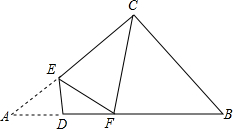    20．如图，在Rt△ABC中，AC=8，BC=6，点D为斜边AB上一点，DE⊥AB交AC于点E，将△AED沿DE翻折，点A的对应点为点F．如果△EFC是直角三角形，那么AD的长为$\frac{7}{5}$或5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

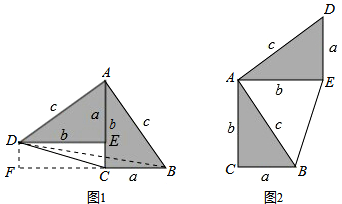    1．勾股定理神秘而美妙，它的证法多样，其巧妙各有不同，其中的“面积法”给了小聪以灵感，他惊喜的发现，当两个全等的直角三角形如图1或图2摆放时，都可以用“面积法”来证明，下面是小聪利用图1证明勾股定理的过程：
    将两个全等的直角三角形按图1所示摆放，其中∠DAB=90°，求证：a2+b2=c2．
    证明：连结DB，过点D作BC边上的高DF，则DF=EC=b-A
    ∵S四边形ADCB=S△ACD+S△ABC=$\frac{1}{2}$b2+$\frac{1}{2}$aB．
    又∵S四边形ADCB=S△ADB+S△DCB=$\frac{1}{2}$c2+$\frac{1}{2}$a（b-a）
    ∴$\frac{1}{2}$b2+$\frac{1}{2}$ab=$\frac{1}{2}$c2+$\frac{1}{2}$a（b-a）
    ∴a2+b2=c2
    请参照上述证法，利用图2完成下面的证明．
    将两个全等的直角三角形按图2所示摆放，其中∠DAB=90°．求证：a2+b2=c2．
    证明：连结BD，过点B作DE边上的高BF，则BF=b-a，
    ∵S五边形ACBED=S△ACB+S△ABE+S△ADE=$\frac{1}{2}$ab+$\frac{1}{2}$b2+$\frac{1}{2}$ab，
    又∵S五边形ACBED=S△ACB+S△ABD+S△BDE=$\frac{1}{2}$ab+$\frac{1}{2}$c2+$\frac{1}{2}$a（b-a），
    ∴$\frac{1}{2}$ab+$\frac{1}{2}$b2+$\frac{1}{2}$ab=$\frac{1}{2}$ab+$\frac{1}{2}$c2+$\frac{1}{2}$a（b-a），
    ∴a2+b2=c2．

    查看答案和解析>>

    同步练习册答案