
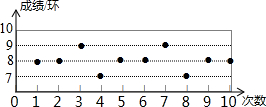
 某射击队要从甲、乙、丙、丁四人中选拔一名选手参赛,在选拔赛中,每人射击10次,然后从他们的成绩平均数(环)及方差两个因素进行分析,甲、乙、丙的成绩分析如表所示,丁的成绩如图所示.
某射击队要从甲、乙、丙、丁四人中选拔一名选手参赛,在选拔赛中,每人射击10次,然后从他们的成绩平均数(环)及方差两个因素进行分析,甲、乙、丙的成绩分析如表所示,丁的成绩如图所示.| 甲 | 乙 | 丙 | |
| 平均数 | 7.9 | 7.9 | 8.0 |
| 方差 | 3.29 | 0.49 | 1.8 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
分析 根据方差的计算公式求出丁的成绩的方差,根据方差的性质解答即可.
解答 解:由图可知丁射击10次的成绩为:8、8、9、7、8、8、9、7、8、8,
则丁的成绩的平均数为:$\frac{1}{10}$×(8+8+9+7+8+8+9+7+8+8)=8,
丁的成绩的方差为:$\frac{1}{10}$×[(8-8)2+(8-8)2+(8-9)2+(8-7)2+(8-8)2+(8-8)2+(8-9)2+(8-7)2+(8-8)2+(8-8)2]=0.4,
∵丁的成绩的方差最小,
∴丁的成绩最稳定,
∴参赛选手应选丁,
故选:D.
点评 本题考查的是方差的概念、性质以及方差的计算,方差的计算公式是:s2=1n[(x1-x?)2+(x2-x?)2+…+(xn-x?)2、方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=5,F为DE的中点.若△CEF的周长为18,则OF的长为$\frac{7}{2}$.
如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=5,F为DE的中点.若△CEF的周长为18,则OF的长为$\frac{7}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 7.1×10-6 | B. | 7.1×10-7 | C. | 1.4×106 | D. | 1.4×107 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
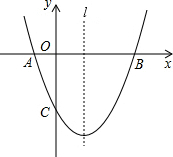 如图,已知抛物线y=ax2+bx+c(a≠0)经过A(-1,0)、B(3,0)、C(0,-3)三点,直线l是抛物线的对称轴.
如图,已知抛物线y=ax2+bx+c(a≠0)经过A(-1,0)、B(3,0)、C(0,-3)三点,直线l是抛物线的对称轴.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,C、D是以线段AB为直径的⊙O上两点,若CA=CD,且∠ACD=40°,则∠CAB=( )
如图,C、D是以线段AB为直径的⊙O上两点,若CA=CD,且∠ACD=40°,则∠CAB=( )| A. | 10° | B. | 20° | C. | 30° | D. | 40° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
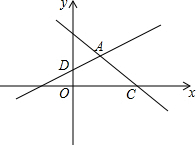 如图,在平面直角坐标系xOy中,直线y=-x+3与x轴交于点C,与直线AD交于点A($\frac{4}{3}$,$\frac{5}{3}$),点D的坐标为(0,1)
如图,在平面直角坐标系xOy中,直线y=-x+3与x轴交于点C,与直线AD交于点A($\frac{4}{3}$,$\frac{5}{3}$),点D的坐标为(0,1)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com