
【题目】如图,在平面直角坐标系中,直线y=kx﹣![]() 与抛物线y=ax2+bx+
与抛物线y=ax2+bx+![]() 交于点A、C,与y轴交于点B,点A的坐标为(2,0),点C的横坐标为﹣8.
交于点A、C,与y轴交于点B,点A的坐标为(2,0),点C的横坐标为﹣8.
(1)请直接写出直线和抛物线的解析式;
(2)点D是直线AB上方的抛物线上一动点(不与点A、C重合),作DE⊥AC于点E.设点D的横坐标为m.求DE的长关于m的函数解析式,并写出DE长的最大值;
(3)平移△AOB,使平移后的三角形的三个顶点中有两个在抛物线上,请直接写出平移后的点A对应点A′的坐标.
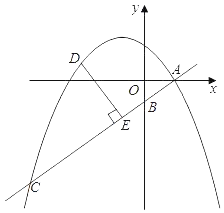
【答案】(1)![]() ;(2)DE的最大值为5;(3)点A′(﹣
;(2)DE的最大值为5;(3)点A′(﹣![]() ,
,![]() )或(﹣2,3)
)或(﹣2,3)
【解析】
(1)将点A,C坐标代入一次函数与二次函数表达式,即可解题,
(2)根据DE= DFsin∠DFE=![]() ·(﹣
·(﹣![]() m2﹣
m2﹣![]() m+4)=﹣
m+4)=﹣![]() (m+3)2+5即可求解,
(m+3)2+5即可求解,
(3)分别设出平移后的点A,B,O的坐标,根据有两个点在二次函数图形上,代入解方程组即可解题.
(1)将点A坐标代入直线表达式得:0=2k﹣![]() ,解得:k=
,解得:k=![]() ,
,
故一次函数表达式为:y=![]() x﹣
x﹣![]() ,则点C坐标为(﹣8,﹣
,则点C坐标为(﹣8,﹣![]() ),
),
同理,将点A、C的坐标代入二次函数表达式并解得二次函数表达式为:![]() ;
;
(2)作DF∥y轴交直线AB于点F,
∴∠DFE=∠OBA,(同角的余角相等)
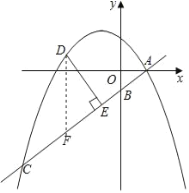
设点D的横坐标为m,则点D(m,﹣![]() m2﹣
m2﹣![]() m+
m+![]() ),点F(m,
),点F(m,![]() m﹣
m﹣![]() ),
),
DF=﹣![]() m2﹣
m2﹣![]() m+
m+![]() ﹣(
﹣(![]() m﹣
m﹣![]() )=﹣
)=﹣![]() m2﹣
m2﹣![]() m+4,
m+4,
AB=![]() =
=![]() ,sin∠DFE=sin∠OBA=
,sin∠DFE=sin∠OBA=![]() ,
,
∴DE=DFsin∠DFE=![]() ·(﹣
·(﹣![]() m2﹣
m2﹣![]() m+4)=﹣
m+4)=﹣![]() (m+3)2+5,
(m+3)2+5,
故:DE的最大值为5;
(3)设三角形向左平移m个、向上平移n个单位时,三角形有2个顶点在抛物线上,
①当平移后点A和O在抛物线上时,
则平移后点A、O的坐标分别为(2﹣m,n)、(﹣m,n),
将上述两个点坐标代入二次函数表达式得:
解得:m=![]() ,n=
,n=![]() ,
,
②当平移后点A和B在抛物线上时,平移后点A、B的坐标分别为(2﹣m,n)、(﹣m,n-![]() ),
),
同理可得:点A′(﹣2,3),
即点A′(﹣![]() ,
,![]() )或(﹣2,3).
)或(﹣2,3).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某市今年中考理化实验操作考试,采用学生抽签方式决定自己的考试内容.规定:每位考生必须在三个物理实验(用纸签A、B、C表示)和三个化学实验(用纸签D、E、F表示)中各抽取一个进行考试,小刚在看不到纸签的情况下,分别从中各随机抽取一个.
(1) 用“列表法”或“树状图法”表示所有可能出现的结果;
(2) 小刚抽到物理实验B和化学实验F(记作事件P)的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大楼AD与塔CB之间的距离AC长为27m,某人在楼底A处测得塔顶的仰角为60°,爬到楼顶D处测得塔顶B的仰角为30°,分别求大楼AD的高与塔BC的高(结果精确到0.1m,参考数据:![]() ≈2.24,
≈2.24,![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是Rt△ABC的外接圆,∠ACB=90°,点D是![]() 上的一点,且
上的一点,且![]() ,连接AD交BC于点F,过点A作⊙O的切线AE交BC的延长线于点E.
,连接AD交BC于点F,过点A作⊙O的切线AE交BC的延长线于点E.
(1)求证:CF=CE;
(2)若AD=8,AC=5,求⊙O的半径.
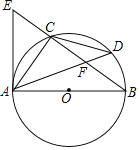
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以![]() 的一边
的一边![]() 为直径的
为直径的![]() 交
交![]() 于点
于点![]() ,点
,点![]() 是弧
是弧![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 于点
于点![]() .
.
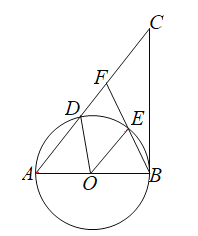
(1)求证:![]() ;
;
(2)①若![]() ,当弧
,当弧![]() 的长度是______时,四边形
的长度是______时,四边形![]() 是菱形;
是菱形;
②在①的情况下,当![]() ______时,
______时,![]() 是
是![]() 的切线.
的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,点O在AB上,BC=CD,过点C作⊙O的切线,分别交AB,AD的延长线于点E,F.
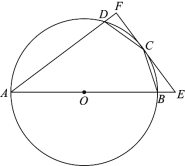
(1)求证:AF⊥EF;(2)若cosA=![]() ,BE=1,求AD的长.
,BE=1,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
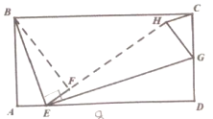
【题目】如图,矩形ABCD中,AB=4,AD=8,点E为AD上一点,将△ABE沿BE折叠得到△FBE,点G为CD上一点,将△DEG沿EG折叠得到△HEG,且E、F、H三点共线,当△CGH为直角三角形时,AE的长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象交
的图象交![]() 轴于点
轴于点![]() ,点
,点![]() ,交
,交![]() 轴于点
轴于点![]()

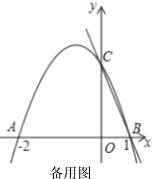
(1)求二次函数的解析式;
(2)连接![]() ,在直线
,在直线![]() 上方的抛物线上有一点
上方的抛物线上有一点![]() ,过点
,过点![]() 作
作![]() 轴的平行线,交直线
轴的平行线,交直线![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,线段
,线段![]() 的长为
的长为![]() ,求
,求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)若点![]() 在
在![]() 轴上,是否存在点
轴上,是否存在点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 为顶点的三角形是等腰三角形,若存在,直接写出点
为顶点的三角形是等腰三角形,若存在,直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com