练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

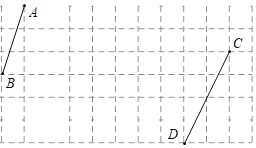
    【题目】如图，在毎个小正方形的边长均为1的方格纸中有线段AB和CD，点A、B、C、D均在小正方形的顶点上．

    （1）画出一个以AB为一直角边的Rt△ABE，点E在小正方形的顶点上，且∠BAE＝45°；

    （2）画出一个以CD为一边的菱形CDMN，点M、N均在小正方形的顶点上，且菱形CDMN的面积是△ABE面积的4倍，连接EN，请直接写出线段EN的长．

    【答案】（1）详见解析；（2）图详见解析，5

    【解析】

    (1)画出一个以AB为一直角边的Rt△ABE，点E在小正方形的顶点上，且∠BAE=45°即可；

    (2)画出一个以CD为一边的菱形CDMN，点M、N均在小正方形的顶点上，且菱形CDMN的面积是△ABE面积的4倍即可．根据勾股定理即可直接写出线段EN的长．

    如图所示：

    (1)Rt△ABE即为所求作的图形，且∠BAE=45°；

    (2)菱形CDMN即为所求作的图形，

    ，

    ，

    ∴菱形CDMN的面积是△ABE面积的4倍．

    连接EN，线段EN的长为5．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】为了抓住文化艺术节的商机，某商店决定购进A、B两种艺术节纪念品．若购进A种纪念品8件，B种纪念品3件，需要950元；若购进A种纪念品5件，B种纪念品6件，需要800元．

    （1）求购进A、B两种纪念品每件各需多少元？

    （2）若该商店决定购进这两种纪念品共100件，考虑市场需求和资金周转，用于购买这100件纪念品的资金不少于7500元，那么该商店至少要购进A种纪念品多少件？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】距离中考体考时间越来越近，年级组想了解初三年级2400名学生周末在家体育锻炼的情况，在初三年级随机抽查了20名男生和20名女生周末每天在家锻炼的时间情况．

    （一）收集数据：（单位：分）

    男生：20 30 40 45 60 120 80 50 100 45 85 90 90 70 90 50 90 50 70 40

    女生：75 30 120 70 60 100 90 40 75 60 75 75 80 90 70 80 50 80 100 90

    （二）整理、描述数据：（表一）

    时间x

    x≤30

    30＜x≤60

    60＜x≤90

    90＜x≤120

    男生

    2

    8

    8

    2

    女生

    1

    4

    a

    3

    （表二）两组数据的极差、平均数、中位数、众数

    极差

    平均数

    中位数

    众数

    男生

    100

    65.75

    b

    c

    女生

    90

    75.5

    75

    75

    （三）分析、应用数据：

    （1）请将上面两个表格补充完整：a＝_____，b＝______，c＝______；

    （2）请根据抽样调查的数据估计初三年级周末每天锻炼时间在100分钟以上（含100分钟）的同学大约有多少人？

    （3）李老师看了表格数据后认为初三年级的女生周末锻炼坚持得比男生好，请你结合统计数据，写出支持老师观点的理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

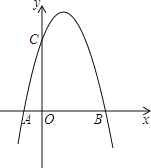
    【题目】如图已知在直角坐标系中，一条抛物线与x轴交于A、B两点，与y轴交于C点，其中B（3，0），C（0，4），点A在x轴的负半轴上，OC＝4OA．

    （1）求点A坐标；

    （2）求这条抛物线的解析式，并求出它的顶点坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，抛物线y＝﹣x2+bx+c交x轴负半轴于点A，交x轴正半轴于点B（4，0），交y轴正半轴于点C，OC＝4OA，S△ABC＝24．

    （1）求抛物线的解析式；

    （2）点P为第一象限抛物线上一点，过点P作PD⊥AB于点D，连接AP交y轴于点E，过点E作EG⊥PD于点G，设点P的横坐标为t（t≤1），PG的长度为d，求d与t之间的函数关系式（不要求写出自变量t的取值范围）；

    （3）在（2）的条件下，过点B作BF⊥EG交EG的延长线于点F，点Q在线段GF上，连接DQ、PQ，将△DGQ沿DQ折叠后，点G的对称点为点H，DH交BF于点M，连接MQ并延长交DP的延长线于点N，当∠DQM＝45°，tan∠PQN＝时，求直线PQ的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示， ，点为内部一点，作射线，点在射线上，且，点与点关于射线对称，且直线与射线交于点．当为等腰三角形时，的长为__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

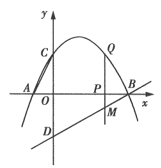
    【题目】如图所示，已知抛物线经过点三点，点与点关于轴对称，点是线段上的一个动点，设点的坐标为过点作轴的垂线交抛物线于点，交直线于点．

    （1）求该抛物线所表示的二次函数的表达式；

    （2）在点运动过程中，是否存在点，使得是直角三角形?若存在，求出点的坐标；若不存在，请说明理由；

    （3）连接，将绕平面内某点顺时针旋转，得到，点的对应点分别是点．若的两个顶点恰好落在抛物线上，那么我们就称这样的点为"和谐点"，请直接写出"和谐点"的个数和点的横坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对于反比例函数，下列说法错误的是（　　）

    A. 函数图象位于第一、三象限

    B. 函数值y随x的增大而减小

    C. 若A（-1，y1）、B（1，y2）、C（2，y3）是图象上三个点，则y1＜y3＜y2

    D. P为图象上任意一点，过P作PQ⊥y轴于Q，则△OPQ的面积是定值

    查看答案和解析>>

    科目：初中数学 来源： 题型：

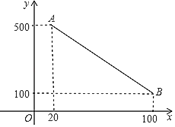
    【题目】小明家买了一台充电式自动扫地机，每次完成充电后，在使用时扫地机会自动根据设定扫地时间，来确定扫地的速度(以使每次扫地结束时尽量把所储存的电量用完)，如图是“设定扫地时间”与“扫地速度”之间的函数图象(线段AB)，其中设定扫地时间为x分钟，扫地速度为y平方分米/分钟．

    (1)求y关于x的函数解析式；

    (2)现在小明需要扫地机完成180平方米的扫地任务，他应该设定的扫地时间为多少分钟？

    查看答案和解析>>

    同步练习册答案