练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    图形的移动，叫做　　　　　　　　　　　　　　 ，简称　　　　　　　　 　　　　　　　　．

    答案：
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：三点一测丛书九年级数学上 题型：059

    全等变换

    　　拿一张纸对折后，剪成两个全等的三角形，把这两个三角形一起放到图中△ABC的位置上．试一试，如果其中一个三角形不动，怎样移动另一个三角形，能够得到图中的各图形：

    　　通过实际操作可以知道：(1)把△ABC沿直线BC移动线段BC那样长的距离，可以变到△ECD的位置；(2)以BC为轴把△ABC翻折，可以变到△DBC的位置；(3)以点A为中心，把△ABC旋转，可以变到△AED的位置．这些图形中的两个三角形之间有这样的关系，其中一个三角形是由另一个三角形按平行移动、翻折或旋转等方法得到的，像这样按一定方法把一个图形变成另一个图形叫做图形变换．

    　　经过图形变换，图形的一些性质改变了，而另一些性质仍然保留下来．上面三个图形经过变换，图形的位置变化了，但形状大小都没有改变，即变换前后的图形全等，像这样只改变图形的位置，而不改变其形状大小的图形变换叫做全等变换．

    　　利用图形变换，可以为研究几何图形提供方便．

    试一试，你能用两个全等三角形拼成图中的各种图形吗？这些图形都可以看成是一个三角形经过全等变换得到的．

    查看答案和解析>>

    科目：初中数学 来源：三点一测丛书八年级数学上 题型：044

    几何变换

    　　平移、对称与旋转是常见的几何变换，它们都是把一个几何图形F1变换成为一个几何图形F2，而且这种变换仅改变图形的位置，不改变图形的形状和大小．

    　　例如：把△ABC沿直线BC平行移动，可以变到△ECD的位置(如图1)；以BC为轴把△ABC翻折，可以变到△BDC的位置(如图2)；绕A点把△ABC逆时针旋转，可以变到△AED的位置(如图3)．

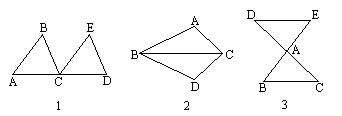
    　　像这样，其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法变成的，这种只改变位置，不改变形状大小的图形变换，叫做三角形的全等变换．

    如图，在正方形ABCD中，E是AD的中点，F是BA的延长线上一点，AF＝AB．

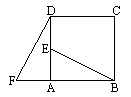
    (1)你认为可以通过平移、翻折、旋转中的哪一种方法，使△ABE变到△ADF的位置，怎样变化？

    (2)根据全等变换的意义，你能否知道线段BE与DF之间的关系．

    查看答案和解析>>

    科目：初中数学 来源：数学教研室 题型：044

    如图①，在正方形ABCD中，E是AD的中点，F是BA延长线上的一点，AF=AB，

    （1）求证：△ABE≌△ADF.

    （2）阅读下列材料：如图②，把△ABC沿直线平移线段BC的长度，可以变到△ECD的位置；如图③，以BC为轴把△ABC翻折180°，可以变到△DBC的位置；如图④，以点A为中心，把△ABC旋转180°，可以变到△AED的位置，像这样其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法变成的，这种只改变位置，不改变形状大小的图形变换，叫做三角形的全等变换.

    　　  图①　　　　　　   图②　　　　　　　　  图③　　　　   图④

    请回答下列问题：

    （1）在图①中，可以通过平移、翻折、旋转中的哪一种方法，使△ABE变到△ADF的位置？

    （2）指出图①中线段BE与DF之间的关系.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在平面内，将一个图形沿某个方向移动一定的距离的图形运动叫做　　　　 ．

    查看答案和解析>>

    同步练习册答案