
分析 (1)根据绝对值、特殊角的三角函数值、零指数幂、负整数指数幂分别求出每一部分的值,再代入求出即可;
(2)先根据方程组求出x+y=3,算乘法,再算减法,最后代入求出即可.
解答 解:(1)原式=$\sqrt{3}$-1+3×$\frac{\sqrt{3}}{3}$-1-(-3)
=$\sqrt{3}$-1+$\sqrt{3}$-1+3
=2$\sqrt{3}$+1;
(2)∵方程组$\left\{\begin{array}{l}{2x-y=1}\\{-x+2y=2}\end{array}\right.$中的两个方程相加得:x+y=3,
∴$\frac{1}{x-1}$•$\frac{{x}^{2}-1}{x+y}$-$\frac{x}{x+y}$
=$\frac{1}{x-1}$•$\frac{(x+1)(x-1)}{x+y}$-$\frac{x}{x+y}$
=$\frac{x+1}{x+y}$-$\frac{x}{x+y}$
=$\frac{1}{x+y}$
=$\frac{1}{3}$.
点评 本题考查了绝对值、特殊角的三角函数值、零指数幂、负整数指数幂,解二元一次方程组,分式的混合运算和求值等知识点,能灵活运用知识点进行化简和计算是解此题的关键.


科目:初中数学 来源: 题型:解答题
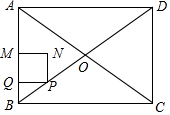 如图,矩形ABCD的对角线相交于点O,AB=6cm,BC=8cm,动点P以1cm/s的速度从点B出发,沿B→O→C向终点C运动,当点P在OB上运动时,过点P作PQ⊥AB于点Q,以PQ为边向上方作正方形PQMN,当点P在OC上运动时,过点P作PQ∥AB交OD于点Q,以PQ为边向左侧作正方形PQMN,设正方形PQMN与△ABO重叠部分图形的面积为S(cm2),点P运动的时间为t(s).
如图,矩形ABCD的对角线相交于点O,AB=6cm,BC=8cm,动点P以1cm/s的速度从点B出发,沿B→O→C向终点C运动,当点P在OB上运动时,过点P作PQ⊥AB于点Q,以PQ为边向上方作正方形PQMN,当点P在OC上运动时,过点P作PQ∥AB交OD于点Q,以PQ为边向左侧作正方形PQMN,设正方形PQMN与△ABO重叠部分图形的面积为S(cm2),点P运动的时间为t(s).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
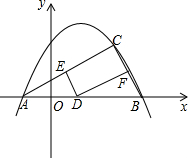 如图,已知抛物线y=-$\frac{1}{2}{x^2}$+bx+c图象经过A(-1,0),B(4,0)两点.
如图,已知抛物线y=-$\frac{1}{2}{x^2}$+bx+c图象经过A(-1,0),B(4,0)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
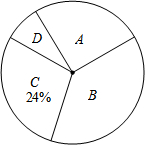 近期电视剧《人民的名义》热播,某校“话剧表演”社团在本校学生中开展学生知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A、B、C、D四类.其中,A类表示“自己看过”,B类表示“听家长讲过”,
近期电视剧《人民的名义》热播,某校“话剧表演”社团在本校学生中开展学生知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A、B、C、D四类.其中,A类表示“自己看过”,B类表示“听家长讲过”,| 类别 | A | B | C | D |
| 频数 | 30 | 40 | 24 | b |
| 频率 | a | 0.4 | 0.24 | 0.06 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
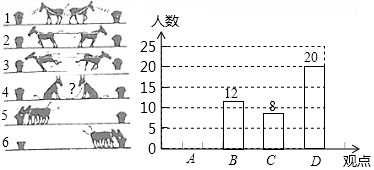 主题班会课上,王老师出示了如图所示的一幅漫画,经过同学们的一番热议,达成以下四个观点:
主题班会课上,王老师出示了如图所示的一幅漫画,经过同学们的一番热议,达成以下四个观点:| 观点 | 频数 | 频率 |
| A | a | 0.2 |
| B | 12 | 0.24 |
| C | 8 | b |
| D | 20 | 0.4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com