
���� ��1�����ݵڢ�����֪���ݶ���2�ij˷��õ��������õ�ż����ϵ��Ϊ�������ɵó��𰸣��������õڢڣ��������1�еĴ�С��ϵ�ó����ɣ�
��2�����ݢ������ݹ�ϵ�ֱ��ʾ��3����������������������ǵĺͣ�
��3��������֪���ɵó��������ݵĹ��ɽ����ó�����������ɣ�
��� �⣺��1����2��-4��8��-16��32��-64������ ��
��21=2��-4=-22��8=23��-16=-24����
��ڢ��е�8����Ϊ��-28=-256��
��4��-2��10��-14��34��-62�������ȵ�һ�ж�Ӧ���ִ�2��
��ڢ��е�8����Ϊ��-254��
��1��-2��4��-8��16��-32��������
��ڢ����ǵ�һ�е�$\frac{1}{2}$��
��ڢ��е�8����Ϊ��-128��
��2�����ڣ�
���3������������-1��n+1��2n-1+��-1��n+2��2n+��-1��n+3��2n+1=768��
��nΪż���������ó���-5����-2��n-1=768������������
��nΪ�����������ó���3��2n-1=768����ã�n=9��
��3������256��-512��1024��
��3�������ڣ�
��ͬһ�е���������ͬ��
��������������������
����һ���������ĺ�Ϊ��2n+2��2n+$\frac{1}{2}$��2n=1282
2n=$\frac{2564}{7}$
�����������һ�У�ʹ�����е��������ĺ�Ϊ1282��
���� ���⿼�����ֵı仯���ɣ��ҳ����ֵı仯���ɣ��ó���֮������㷽��������⣮


 �������Ͽ��㱾ϵ�д�
�������Ͽ��㱾ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | -4 | C�� | ��4 | D�� | ��ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
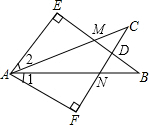 ��֪��ͼ����E=��F=90�㣬��B=��C��AE=AF��
��֪��ͼ����E=��F=90�㣬��B=��C��AE=AF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
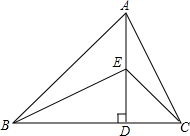 ��֪����ͼ��AD��BC������ΪD��AD=BD����E��AD�ϣ���ABD=��CED=45�㣬��ABE=��ACE����д��ͼ����ȵ��߶Σ�������֤����
��֪����ͼ��AD��BC������ΪD��AD=BD����E��AD�ϣ���ABD=��CED=45�㣬��ABE=��ACE����д��ͼ����ȵ��߶Σ�������֤�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
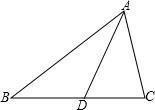 ��ͼ����ABC�У���BAC=54�㣬��B=46�㣬AD�ǡ�BAC�Ľ�ƽ���ߣ����ADC����ADB�Ķ�����
��ͼ����ABC�У���BAC=54�㣬��B=46�㣬AD�ǡ�BAC�Ľ�ƽ���ߣ����ADC����ADB�Ķ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=4x2-8x-7 | B�� | y=4x2-8x+1 | C�� | y=2x2-4x+1 | D�� | y=-2x2-4x+1 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com