
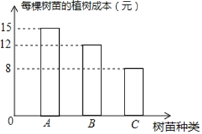
【题目】现种植A、B、C三种树苗一共480棵,安排80名工人一天正好完成,已知每名工人只植一种树苗,且每名工人每天可植A种树苗8棵;或植B种树苗6棵,或植C种树苗5棵.经过统计,在整个过程中,每棵树苗的种植成本如图所示.
设种植A种树苗的工人为x名,种植B种树苗的工人为y名.
(1)求y与x之间的函数关系式;
(2)若种植的总成本为5600元,从植树工人中随机采访一名工人,求采访到种植C种树苗工人的概率.
【答案】(1)y=﹣3x+80;(2)![]() .
.
【解析】
(1)先求出种植C种树苗的人数,根据现种植A、B、C三种树苗一共480棵,可以列出等量关系,解出y与x之间的关系;
(2)求出种植C种树苗工人的人数,然后用种植C种树苗工人的人数÷总人数即可求出概率.
解:(1)设种植A种树苗的工人为x名,种植B种树苗的工人为y名,则种植C种树苗的人数为(80﹣x﹣y)人,
根据题意,得:8x+6y+5(80﹣x﹣y)=480,
整理,得:y=﹣3x+80
(2)5600=15×8x+12×6y+8×5(80﹣x﹣y)=80x+32y+3200,把y=﹣3x+80带入,得:5600=﹣16x+5760,
解得x=10,y=﹣3×10+80=50,
即种植A种树苗的工人为10名,种植B种树苗的工人为50名,种植C种树苗的工人为:80﹣10﹣50=20名.
采访到种植C种树苗工人的概率为:![]() .
.


科目:初中数学 来源: 题型:
【题目】下列图形都是由同样大小的菱形按照一定规律组成的,请根据排列规律完成下列问题:
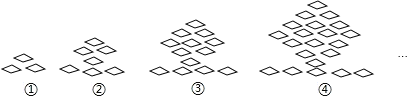
(1)填写下表:
图形序号 | 菱形个数 |
| 3 |
| 7 |
| ______ |
| ______ |
|
|
(2)根据表中规律猜想,图n中菱形的个数![]() 用含n的式子表示,不用说理
用含n的式子表示,不用说理![]() ;
;
(3)是否存在一个图形恰好由91个菱形组成?若存在,求出图形的序号;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们可以用![]() 表示
表示![]() 为自变量的函数,如一次函数
为自变量的函数,如一次函数![]() ,可表示
,可表示![]() ,
,![]() ,
,![]() .
.
(1)已知二次函数![]() ;
;
①求证:不论![]() 为何值,此函数图像与
为何值,此函数图像与![]() 轴总有两个交点;
轴总有两个交点;
②若![]() ,是否存在实数
,是否存在实数![]() ,使得当
,使得当![]() 时,函数
时,函数![]() 的最小值为
的最小值为![]() ,若存在,求出
,若存在,求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(2)已知函数![]() ,
,![]() ,若实数
,若实数![]() 、
、![]() 使得
使得![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,已知抛物线![]() (a<0)与x轴交于A、B两点(点A在点B左侧),与y轴负半轴交于点C,顶点为D,已知
(a<0)与x轴交于A、B两点(点A在点B左侧),与y轴负半轴交于点C,顶点为D,已知![]() :S四边形ACBD=1:4.
:S四边形ACBD=1:4.
(1)求点D的坐标(用仅含c的代数式表示);
(2)若tan∠ACB=![]() ,求抛物线的解析式.
,求抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与坐标轴分别交于A,B,C,点D在x轴上,AC=CD,过点D作DE⊥x轴交抛物线于点E,点P,Q分别是线段CO,CD上的动点,且CP=QD.记△APC的面积为S1,△PCQ的面积为S2,△QED的面积为S3,
与坐标轴分别交于A,B,C,点D在x轴上,AC=CD,过点D作DE⊥x轴交抛物线于点E,点P,Q分别是线段CO,CD上的动点,且CP=QD.记△APC的面积为S1,△PCQ的面积为S2,△QED的面积为S3,
(1)若S1+S3=4S2 ,求Q点坐标;
(2)连结AQ,求AP+AQ的最小值;
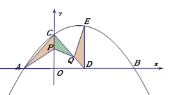
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形△ABC中,∠BAC=120°,AB=3.
(1)求BC的长.
(2)如图,点D在CA的延长线上,DE⊥AB于E,DF⊥BC于F,连EF.求EF的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北京第一条地铁线路于1971年1月15日正式开通运营.截至2017年1月,北京地铁共“金山银山,不如绿水青山”.某市不断推进“森林城市”建设,今春种植四类树苗,园林部门从种植的这批树苗中随机抽取了4000棵,将各类树苗的种植棵数绘制成扇形统计图,将各类树苗的成活棵数绘制成条形统计图,经统计松树和杨树的成活率较高,且杨树的成活率为97%,根据图表中的信息解答下列问题:
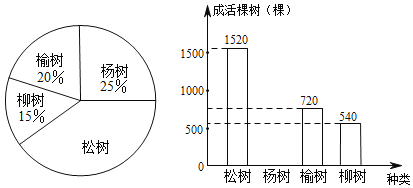
(1)扇形统计图中松树所对的圆心角为 度,并补全条形统计图.
(2)该市今年共种树16万棵,成活了约多少棵?
(3)园林部门决定明年从这四类树苗中选两类种植,请用列表法或树状图求恰好选到成活率较高的两类树苗的概率.(松树、杨树、榆树、柳树分别用A,B,C,D表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
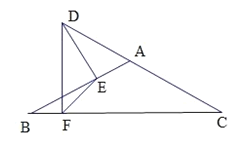
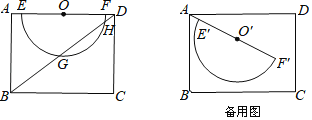
【题目】如图,在矩形ABCD中,AB=6,BC=8,O是AD的中点,以O为圆心在AD的下方作半径为3的半圆O,交AD于E、F.
思考:连接BD,交半圆O于G、H,求GH的长;
探究:将线段AF连带半圆O绕点A顺时针旋转,得到半圆O′,设其直径为E'F′,旋转角为α(0<α<180°).
(1)设F′到AD的距离为m,当m>![]() 时,求α的取值范围;
时,求α的取值范围;
(2)若半圆O′与线段AB、BC相切时,设切点为R,求![]() 的长.
的长.
(sin49°=![]() ,cos41°=
,cos41°=![]() ,tan37°=
,tan37°=![]() ,结果保留π)
,结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
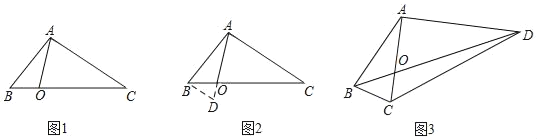
【题目】如图,(1)某学校“智慧方园”数学社团遇到这样一个题目:如图1,在△ABC中,点O在线段BC上,∠BAO=20°,∠OAC=80°,AO=![]() ,BO:CO=1:3,求AB的长.经过社团成员讨论发现,过点B作BD∥AC,交AO的延长线于点D,通过构造△ABD就可以解决问题(如图2),请回答:∠ADB= °,AB= .
,BO:CO=1:3,求AB的长.经过社团成员讨论发现,过点B作BD∥AC,交AO的延长线于点D,通过构造△ABD就可以解决问题(如图2),请回答:∠ADB= °,AB= .
(2)请参考以上思路解决问题:如图3,在四边形ABCD中,对角线AC、BD相交于点O,AC⊥AD,AO=6![]() ,∠ABC=∠ACB=75°,BO:OD=1:3,求DC的长.
,∠ABC=∠ACB=75°,BO:OD=1:3,求DC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com