
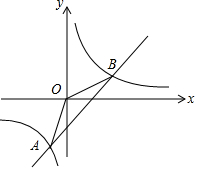
 如图,函数y=$\frac{k}{x}$与y=ax-1的图象的交点分别为A(-1,n),B(2,1).
如图,函数y=$\frac{k}{x}$与y=ax-1的图象的交点分别为A(-1,n),B(2,1).分析 (1)利用待定系数法即可求得反比例函数的解析式,然后求得a和n的值;
(2)利用待定系数法求得AB的解析式,进而求得AB的x轴的交点,然后利用三角形的面积公式求解;
(3)反比例函数值大于一次函数值时对应的x的取值范围就是反比例函数的图象在一次函数的图象的上边时对应的x的取值范围.
解答 解:(1)把(2,1)代入y=$\frac{k}{x}$得k=2×1=2,
则函数的解析式是y=$\frac{2}{x}$,
把x=-1代入n=$\frac{2}{x}$得n=-2;
把(2,1)代入y=ax-1得2a-1=1,
解得a=1;
(2)设AB的解析式是y=kx+b,
则$\left\{\begin{array}{l}{-k+b=-2}\\{2k+b=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{b=-1}\end{array}\right.$,
则直线的解析式是y=x+1,
当y=0时,x=1,则求直线与x轴交点的坐标是(1,0).
则S△AOB=$\frac{1}{2}$×1×1+$\frac{1}{2}$×1×2=$\frac{3}{2}$;
(3)x的范围是x<-1或0<x<2.
点评 本题考查了用待定系数法求出函数解析式,一次函数和反比例函数的图象和性质,三角形面积的应用,主要考查学生的计算能力.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
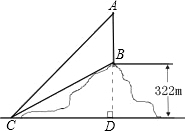 江郎山位我国典型的丹霞地貌景观,被称为“中国丹霞第一奇峰”.要测量三块巨石中的最左边的“郎峰”的高度,在山脚的平地上选取一处观测点C,测得∠BCD=30°,∠ACD=45°,已知从观测点C到“郎峰”脚B的垂直高度为322米,如图所示,那么“郎峰”AB的高度约为多少?
江郎山位我国典型的丹霞地貌景观,被称为“中国丹霞第一奇峰”.要测量三块巨石中的最左边的“郎峰”的高度,在山脚的平地上选取一处观测点C,测得∠BCD=30°,∠ACD=45°,已知从观测点C到“郎峰”脚B的垂直高度为322米,如图所示,那么“郎峰”AB的高度约为多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
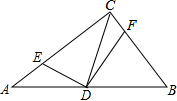 如图,在△ABC中,点D是AB的中点,连接CD,CD=BD,tan∠CDB=$\frac{24}{7}$,在BC上取一点F,使BF=$\frac{1}{2}$AB,连接DF,过点D作DE⊥DF交AC于点E,且AE=1,则BC=$\frac{12}{5}$.
如图,在△ABC中,点D是AB的中点,连接CD,CD=BD,tan∠CDB=$\frac{24}{7}$,在BC上取一点F,使BF=$\frac{1}{2}$AB,连接DF,过点D作DE⊥DF交AC于点E,且AE=1,则BC=$\frac{12}{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com