
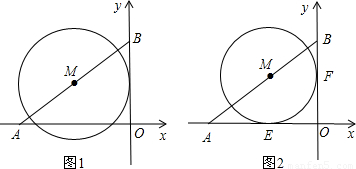
 x+3,根据切线的性质得到点M到x轴、y轴的距离都相等,设M(a,-a)(-4<a<0).代入y=
x+3,根据切线的性质得到点M到x轴、y轴的距离都相等,设M(a,-a)(-4<a<0).代入y= x+3,即可求得a的值,即得到M的坐标.
x+3,即可求得a的值,即得到M的坐标. 解:(1)直线OB与⊙M相切.
解:(1)直线OB与⊙M相切.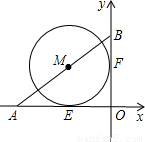
 x+3,
x+3, x+3,
x+3, a+3,得a=-
a+3,得a=-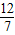 .
.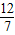 ,
,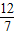 ).
).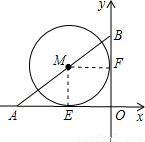 解法二:连接ME、MF.
解法二:连接ME、MF. x+3,
x+3, x,所以AO=
x,所以AO= x.
x. x=4.
x=4.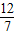 .
. ,
,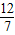 ).
).

 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
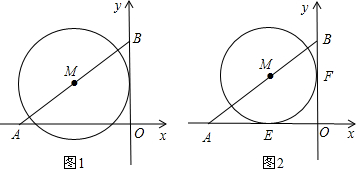
查看答案和解析>>
科目:初中数学 来源:2013年江苏省南京市综合体中考数学一模试卷(解析版) 题型:解答题
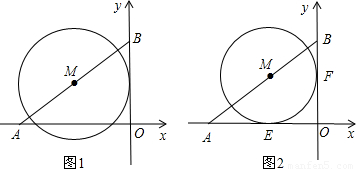
查看答案和解析>>
科目:初中数学 来源:2012年5月中考数学模拟试卷(61)(解析版) 题型:解答题
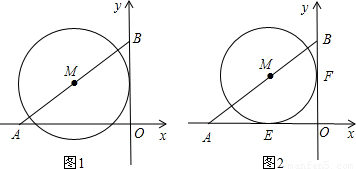
查看答案和解析>>
科目:初中数学 来源:2010-2011学年上海市考数学模拟试卷 题型:解答题
(10分)如图直角坐标系中,已知A(-4,0),B(0,3),点M在线段A
上.
(1)如图1,如果点M是线段AB的中点,且⊙M的半径为2,试判断直线OB与⊙M的位置关系,并说明理由;
(2)如图2,⊙M与x轴、y轴都相切,切点分别是点E、F,试求出点M的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com