
在平面直角坐标系中给定以下五个点A(-3,0),B(-1,4),C(0,3),D(![]() ,
,![]() ),E(1,0).
),E(1,0).

(1)请从五点中任选三点,求一条以平行于y轴的直线为对称轴的抛物线的表达式;
(2)求该抛物线的顶点坐标和对称轴,并画出草图;
(3)已知点F(-1,![]() )在抛物线的对称轴上,直线y=
)在抛物线的对称轴上,直线y=![]() 过点G(-1,
过点G(-1,![]() )且垂直于对称轴.验证:以点E(1,0)为圆心,EF为半径的圆与直线y=
)且垂直于对称轴.验证:以点E(1,0)为圆心,EF为半径的圆与直线y=![]() 相切.请你进一步验证,以抛物线上的点D(
相切.请你进一步验证,以抛物线上的点D(![]() ,
,![]() )为圆心,DF为半径的圆也与直线y=
)为圆心,DF为半径的圆也与直线y=![]() 相切.由此你能猜想到怎样的结论2.
相切.由此你能猜想到怎样的结论2.
|
解:(1)设抛物线的表达式为y=ax2+bx+c, 且过点A(-3,0),C(0,3),E(1,0), 得方程组 所以抛物线的解析式为y=-x2-2x+3. (2)由y=-x2-2x+3=-(x+1)2+4得顶点坐标为 (-1,4),对称轴为x=-1. (3)①连接EF,过点E作直线y= 在Rt△FHE中,HE=2,HF= 所以EF= 所以EF=EN. 所以以E点为圆心,EF为半径的⊙E与直线y= ②连接DF,过点D作直线y=
则DM=QG= 在Rt△FQD中,QD= QF= FD= 所以以D点为圆心,DF为半径的⊙D与直线y= ③以抛物线上任意一点P为圆心,以PF为半径的圆与直线y= 点评:本题(3)问中的结论不唯一,它给定已知条件,但是结论不确定,解答这类问题时,一定要抓住图象特征多角度展开分析,一定要注意准确画图. |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
| ||||
| a+2 |
| k |
| 2 |
| k |
| 2 |
| PM+PN |
| NM |
| PM-PN |
| AM |

查看答案和解析>>
科目:初中数学 来源: 题型:
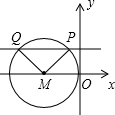 如图,在平面直角坐标系中,⊙M与y轴相切于原点O,平行于x轴的直线交⊙M于P,Q两点,点P在点Q的右方,若点P的坐标是(-1,2),有下列结论:①点Q的坐标是(-4,2);②PQ=3;③△MPQ的面积是3;④M点的坐标是(-3,0).其中正确的结论序号是
如图,在平面直角坐标系中,⊙M与y轴相切于原点O,平行于x轴的直线交⊙M于P,Q两点,点P在点Q的右方,若点P的坐标是(-1,2),有下列结论:①点Q的坐标是(-4,2);②PQ=3;③△MPQ的面积是3;④M点的坐标是(-3,0).其中正确的结论序号是查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•安庆二模)在平面直角坐标系中.过一点分別作x轴与y轴的垂线,若与坐标轴围成矩形的周长与面积相等,则这个点叫做和谐点.给出以下结论:①点M(2,4)是和谐点;②不论a为何值时,点P(2,a)不是和谐点;③若点P(a,3)是和谐点,则a=6;④若点F是和谐点,则点F关于坐标轴的对称点也是和谐点.正确结论的序号是
(2013•安庆二模)在平面直角坐标系中.过一点分別作x轴与y轴的垂线,若与坐标轴围成矩形的周长与面积相等,则这个点叫做和谐点.给出以下结论:①点M(2,4)是和谐点;②不论a为何值时,点P(2,a)不是和谐点;③若点P(a,3)是和谐点,则a=6;④若点F是和谐点,则点F关于坐标轴的对称点也是和谐点.正确结论的序号是查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•老河口市模拟)如图,在平面直角坐标系中,抛物线y=ax2+bx+c交y轴于A(0,4),交x轴于B、C两点(点B在点C的左侧).B、C两点坐标分别为(3,0),(8,0).
(2012•老河口市模拟)如图,在平面直角坐标系中,抛物线y=ax2+bx+c交y轴于A(0,4),交x轴于B、C两点(点B在点C的左侧).B、C两点坐标分别为(3,0),(8,0).查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com