
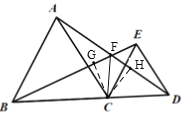
【题目】已知,如图△ABC和△CDE均为等边三角形,B、C、D三点在同一条直线上,连接线段BE、AD交于点F,连接CF,

(1)求证:∠FBC=∠FAC.
(2)求∠BFC的度数.
【答案】(1)证明见解析;(2)∠BFC=60°.
【解析】
(1)根据等边三角形的性质可得∠ECD=∠ABC=60°,AC=BC,CD=CE,利用角的和差关系可得∠ACD=∠BCE,利用SAS可证明△ACD≌△BCE,根据全等三角形的性质即可得答案;(2)作CG⊥BE于G,CH⊥AD于H,由∠ACB=∠EDC=60°可得AC//ED,根据平行线的性质可得∠CAD=∠ADE,利用等量代换可得∠EBD=∠ADE,根据三角形外角性质可得∠EFD=∠EBD+∠BDF=∠ADE+∠BDF=∠BDE=60°,根据平角的定义可得∠BFD=120°,由(1)得△ACD≌△BCE,根据全等三角形对应边上的高对应相等可得CG=CH,根据角平分线的性质可得CF是∠BFD的角平分线,即可求出∠BFC的度数.
(1)∵△ABC和△CDE均为等边三角形,
∴AC=BC,∠ACB=∠ECD=60°,CD=CE,
∴∠ACB+∠ACE=∠ECD+∠ACE,即∠ACD=∠BCE,
在△ACD和△BCE中,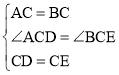 ,
,
∴△ACD≌△BCE,
∴∠EBC=∠DAC,即∠FBC=∠FAC.
(2)∵∠ACB=∠EDC=60°,
∴AC//DE,
∴∠CAD=∠ADE,
∵∠CAD=∠EBD,
∴∠EBD=∠ADE,
∴∠EFD=∠EBD+∠BDF=∠ADE+∠BDF=∠EDB=60°,
∴∠BFD=180°-∠EFD=120°,
∵△ACD≌△BCE,CG、CH分别是对应边BE、AD的高,
∴CG=CH,
∴CF是∠BFD的角平分线,
∴∠BFC=![]() ∠BFD=60°.
∠BFD=60°.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,反比例函数![]() (x>0)与正比例函数y=kx、
(x>0)与正比例函数y=kx、 ![]() (k>1)的图象分别交于点A、B,若∠AOB=45°,则△AOB的面积是________.
(k>1)的图象分别交于点A、B,若∠AOB=45°,则△AOB的面积是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】海水养殖是莱州经济产业的亮丽名片之一,某养殖场响应山东省加快新旧动能转换的号召,今年采用新技术投资养殖了200万笼扇贝,并且全部被订购,已知每笼扇贝的成本是40元,售价是100元,打捞出售过程中发现,一部分扇贝生长情况不合要求,最后只能按照25元一笼出售,如果纯收入为![]() 万元,不合要求的扇贝有
万元,不合要求的扇贝有![]() 万笼.
万笼.
(1)求纯收入![]() 关于
关于![]() 的关系式.
的关系式.
(2)当![]() 为何值时,养殖场不赔不嫌?
为何值时,养殖场不赔不嫌?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:正方形ABCD,点E在CB的延长线上,连接AE、DE,DE与边AB交于点F,FG∥BE交AE于点G.
(1)求证:GF=BF;
(2)若EB=1,BC=4,求AG的长;
(3)在BC边上取点M,使得BM=BE,连接AM交DE于点O.求证:FOED=ODEF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,D、E分别是BC、AC上的动点且BD=CE,连接AD与BE相交于点F,连接CF,下列结论:①△ABD≌△BCE;②∠AFB=120°;③若BD=CD,则FA=FB=FC;④∠AFC=90°,则AF=3BF,其中正确的结论共有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小慧家与文具店相距720米,小慧从家出发,匀速步行12分钟来到文具店,买文具用时4分钟,因家中有事,沿原路匀速跑步返回家中,用时6分钟.
(1)小慧返回家中的速度比去文具店的速度快 米/分钟;
(2)请你画出这个过程中,小慧离家的距离![]() 与时间
与时间![]() 的函数图象;
的函数图象;
(3)求小慧从家出发后经过多少分钟与她家距离为480米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,且
,且![]() 面积是24,
面积是24,![]() 的垂直平分线
的垂直平分线![]() 分别交
分别交![]() 边于点
边于点![]() ,若点
,若点![]() 为
为![]() 边的中点,点
边的中点,点![]() 为线段
为线段![]() 上一动点,则
上一动点,则![]() 周长的最小值为( )
周长的最小值为( )

A.9B.10C.11D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
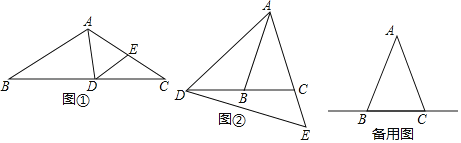
【题目】如图,△ABC中,∠ABC=∠ACB,点D在BC所在的直线上,点E在射线AC上,且AD=AE,连接DE.
⑴如图①,若∠B=∠C=35°,∠BAD=80°,求∠CDE的度数;
⑵如图②,若∠ABC=∠ACB=75°,∠CDE=18°,求∠BAD的度数;
⑶当点D在直线BC上(不与点B、C重合)运动时,试探究∠BAD与∠CDE的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校是乒乓球体育传统项目校,为进一步推动该项目的发展.学校准备到体育用品店购买甲、乙两种型号乒乓球若干个,已知3个甲种乒乓球和5个乙种乒乓球共需50元,2个甲种乒乓球和3个乙种乒乓球共需31元.
(1)求1个甲种乒乓球和1个乙种乒乓球的售价各是多少元?
(2)学校准备购买这两种型号的乒乓球共200个,要求甲种乒乓球的数量不超过乙种乒乓球的数量的3倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com