
【题目】已知点A(a,b)在双曲线y= ![]() 上,若a、b都是正整数,则图象经过B(a,0)、C(0,b)两点的一次函数的解析式(也称关系式)为 .
上,若a、b都是正整数,则图象经过B(a,0)、C(0,b)两点的一次函数的解析式(也称关系式)为 .
【答案】y=﹣5x+5或y=﹣ ![]() x+1
x+1
【解析】∵点A(a,b)在双曲线y= ![]() 上,
上,
∴ab=5,
∵a、b都是正整数,
∴a=1,b=5或a=5,b=1.
设经过B(a,0)、C(0,b)两点的一次函数的解析式为y=mx+n.
①当a=1,b=5时,
由题意,得 ![]() ,解得
,解得 ![]() ,
,
∴y=﹣5x+5;
②当a=5,b=1时,
由题意,得 ![]() ,解得
,解得 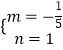 ,
,
∴y=﹣ ![]() x+1.
x+1.
则所求解析式为y=﹣5x+5或y=﹣ ![]() x+1.
x+1.
所以答案是:y=﹣5x+5或y=﹣ ![]() x+1.
x+1.
【考点精析】根据题目的已知条件,利用确定一次函数的表达式的相关知识可以得到问题的答案,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC的垂直平分线分别交AC、BC于E,D两点,EC=4,△ABC的周长为23,则△ABD的周长为( ) 
A.13
B.15
C.17
D.19
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的对角线相交于点O,且点O是BD的中点,若AB=AD=5,BD=8,∠ABD=∠CDB,则四边形ABCD的面积为( )

A.40B.24C.20D.15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A在函数y1=﹣ ![]() (x>0)的图象上,点B在直线y2=kx+1+k(k为常数,且k≥0)上.若A,B两点关于原点对称,则称点A,B为函数y1 , y2图象上的一对“友好点”.请问这两个函数图象上的“友好点”对数的情况为( )
(x>0)的图象上,点B在直线y2=kx+1+k(k为常数,且k≥0)上.若A,B两点关于原点对称,则称点A,B为函数y1 , y2图象上的一对“友好点”.请问这两个函数图象上的“友好点”对数的情况为( )
A.有1对或2对
B.只有1对
C.只有2对
D.有2对或3对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织了全校1500名学生参加传统文化知识网络竞赛.赛后随机抽取了其中200名学生的成绩作为样本进行整理,并制作了如下不完整的频数分布表和频数分布直方图.
成绩(分) | 频数(人) | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 20 | n |
70≤x<80 | m | 0.15 |
80≤x<90 | 80 | 0.40 |
90≤x<100 | 60 | 0.30 |
请根据图表提供的信息,解答下列各题:
(1)表中m= ,n= ,请补全频数分布直方图;
(2)若用扇形统计图来描述成绩分布情况,则分数段80≤x<90对应扇形的圆心角的度数是 ;
(3)若成绩在80分以上(包括80分)为合格,则参加这次竞赛的1500名学生中成绩合格的大约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
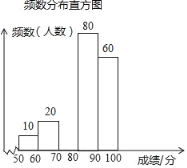
【题目】如图,在平面直角坐标系 ![]() 中,已知直线
中,已知直线 ![]() (
( ![]() )分别交反比例函数
)分别交反比例函数 ![]() 和
和 ![]() 在第一象限的图象于点
在第一象限的图象于点 ![]() ,
, ![]() ,过点
,过点 ![]() 作
作 ![]() 轴于点
轴于点 ![]() ,交
,交 ![]() 的图象于点
的图象于点 ![]() ,连结
,连结 ![]() .若
.若 ![]() 是等腰三角形,则
是等腰三角形,则 ![]() 的值是 .
的值是 . 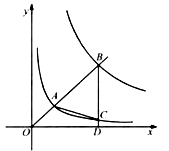
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,抛物线y=ax2+bx+c的顶点为B(﹣1,3),与x轴的交点A在点(﹣3,0)和(﹣2,0)之间,以下结论:
①b2﹣4ac=0;②a+b+c>0;③2a﹣b=0;④c﹣a=3
其中正确的有( )个.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在直角坐标系中,

(1)请写出△ABC各点的坐标.
(2)求出△ABC的面积.
(3)若把△ABC向上平移2个单位,再向右平移2个单位得到△A′B′C′,请在图中画出△A′B′C′,并写出点A′、B′、C′的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com