
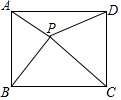
 如图,点P是矩形ABCD内一点,连接PA、PB、PC、PD,已知AB=3,BC=4,设△PAB、△PBC、△PDA的面积分别为S1、S2、S3、S4,以下判断:
如图,点P是矩形ABCD内一点,连接PA、PB、PC、PD,已知AB=3,BC=4,设△PAB、△PBC、△PDA的面积分别为S1、S2、S3、S4,以下判断:分析 ①当点P是矩形ABCD两对角线的交点时,PA+PB+PC+PD的值最小,根据勾股定理可得PA+PB+PC+PD的最小值,即可判断;
②根据全等三角形的性质可得PA=PC,PB=PD,那么P在线段AC、BD的垂直平分线上,即P是矩形ABCD两对角线的交点,易证△PAD≌△PBC,即可判断;
③易证S1+S3=S2+S4,所以若S1=S2,则S3=S4,即可判断;
④根据相似三角形的性质可得∠PAB=∠PDA,∠PAB+∠PAD=∠PDA+∠PAD=90°,利用三角形内角和定理得出∠APD=180°-(∠PDA+∠PAD)=90°,同理可得∠APB=90°,那么∠BPD=180°,即B、P、D三点共线,根据三角形面积公式可得PA=2.4,即可判断.
解答 解:①当点P是矩形ABCD两对角线的交点时,PA+PB+PC+PD的值最小,根据勾股定理得,AC=BD=5,所以PA+PB+PC+PD的最小值为10,故①正确;
②若△PAB≌△PCD,则PA=PC,PB=PD,所以P在线段AC、BD的垂直平分线上,即P是矩形ABCD两对角线的交点,所以△PAD≌△PBC,故②正确;
③若S1=S2,易证S1+S3=S2+S4,则S3=S4,故③正确;
④若△PAB~△PDA,则∠PAB=∠PDA,∠PAB+∠PAD=∠PDA+∠PAD=90°,∠APD=180°-(∠PDA+∠PAD)=90°,同理可得∠APB=90°,那么∠BPD=180°,B、P、D三点共线,P是直角△BAD斜边上的高,根据面积公式可得PA=2.4,故④正确.
故答案为①②③④.
点评 本题考查了轴对称-最短路线问题,全等三角形、相似三角形的性质,勾股定理,矩形的性质,线段垂直平分线的判定等知识,综合性较强,难度适中.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
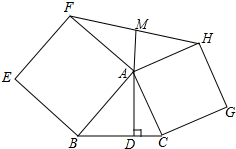 如图,在△ABC的两边AB,AC上向△ABC外作正方形ABEF,ACGH,过点A作BC的垂线分别交BC于点D,交FH于点M,求证:FM=MH.
如图,在△ABC的两边AB,AC上向△ABC外作正方形ABEF,ACGH,过点A作BC的垂线分别交BC于点D,交FH于点M,求证:FM=MH.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 不变 | B. | 扩大3倍 | C. | 缩小3倍 | D. | 扩大9倍 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
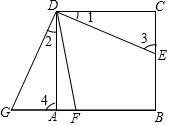 如图,正方形ABCD中,E在BC上,F在AB上且∠FDE=45°,△DEC按顺时针方向转动一个角度后成△DGA.
如图,正方形ABCD中,E在BC上,F在AB上且∠FDE=45°,△DEC按顺时针方向转动一个角度后成△DGA.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
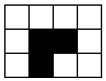 如图,在3×4长方形网格中,黑色部分的图形构成一个轴对称图形.现在任意选取一个白色的小正方形并涂黑,使黑色部分的图形仍然构成一个轴对称图形的概率是$\frac{4}{9}$.
如图,在3×4长方形网格中,黑色部分的图形构成一个轴对称图形.现在任意选取一个白色的小正方形并涂黑,使黑色部分的图形仍然构成一个轴对称图形的概率是$\frac{4}{9}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{12}{13}$ | B. | $\frac{5}{12}$ | C. | $\frac{13}{5}$ | D. | $\frac{5}{13}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com