
如图所示⊙O的直径DF与弦AB交于点E,C为⊙O外一点,CB⊥AB,G是直线CD上一点,∠ADG=∠ABD,求证:AD·CE=DE·DF.
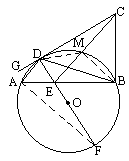
(说明:(1)如果你经历反复探索,没有找到解决问题地方法,请你把探索过程中的某种思维推导过程写出来,(要求至少写3步).(2)在你历经说明(1)的过程之后,可以从下列①、②、③中选取一个补充或更换已知条件,完成你的证明.)
①∠CDB=∠CEB;②AD∥EC;③∠DEC=∠ADF,且∠CDE=90“
|
名师导引:关键是证∠ABD=∠DCE,连AF证∠DCE=∠DBE是难点,∵Rt△CDE与Rt△CBE有公共斜边,∴有公共外接圆. 解答:如图,连结AF,则∠ABD=∠F,而∠ADG=∠ABD,∴∠ADG=∠F,又∵DF为⊙O直径,∴∠DAF= (一)写出探索过程: 如图;连接AF.∵DF为⊙O直径,∴∠DAF= (二)选取①证明,如图,连接AF,则∠ABD=∠F.
∵∠ADG=∠ABD,∴∠ADG=∠F,又∵DF是⊙O直径,∴∠DAF= (三)选取②,如图连接AF,得∠DAF=∠CDE= |


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
(本题满分11分)
如图所示,⊙![]() 的直径
的直径![]() ,
,![]() 和
和![]() 是它的两条切线,
是它的两条切线,![]() 为射线
为射线![]() 上的动点(不与
上的动点(不与![]() 重合),
重合),![]() 切⊙
切⊙![]() 于
于![]() ,交
,交![]() 于
于![]() ,设
,设![]() .
.

(1)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)若⊙![]() 与⊙
与⊙![]() 外切,且⊙
外切,且⊙![]() 分别与
分别与![]()
相切于点![]() ,求
,求![]() 为何值时⊙
为何值时⊙![]() 半径为1.
半径为1.
查看答案和解析>>
科目:初中数学 来源: 题型:
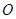 的直径
的直径 ,
, 和
和 是它的两条切线,
是它的两条切线,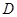 为射线
为射线 上的动点(不与
上的动点(不与 重合),
重合), 切⊙
切⊙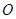 于
于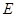 ,交
,交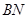 于
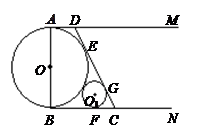
于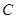 ,设
,设 .
.
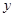 与
与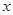 的函数关系式;
的函数关系式;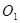 与⊙
与⊙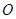 外切,且⊙
外切,且⊙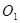 分别与
分别与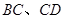
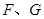 ,求
,求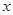 为何值时⊙
为何值时⊙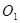 半径为1.
半径为1.查看答案和解析>>
科目:初中数学 来源:2012届广西省贵港市九年级第一次教学质量监测数学卷 题型:解答题
(本题满分11分)
如图所示,⊙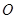 的直径
的直径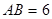 ,
,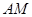 和
和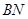 是它的两条切线,
是它的两条切线,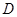 为射线
为射线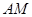 上的动点(不与
上的动点(不与 重合),
重合),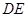 切⊙
切⊙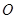 于
于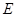 ,交
,交 于
于 ,设
,设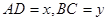 .
.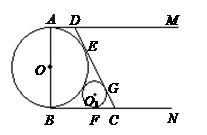
(1)求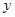 与
与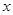 的函数关系式;
的函数关系式;
(2)若⊙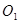 与⊙
与⊙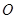 外切,且⊙
外切,且⊙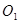 分别与
分别与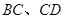
相切于点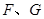 ,求
,求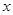 为何值时⊙
为何值时⊙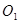 半径为1.
半径为1.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年广西省贵港市九年级第一次教学质量监测数学卷 题型:解答题
(本题满分11分)
如图所示,⊙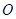 的直径
的直径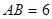 ,
,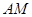 和
和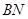 是它的两条切线,
是它的两条切线,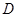 为射线
为射线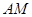 上的动点(不与
上的动点(不与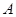 重合),
重合),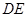 切⊙
切⊙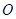 于
于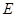 ,交
,交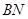 于
于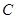 ,设
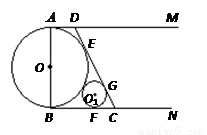
,设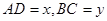 .
.
(1)求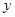 与
与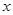 的函数关系式;
的函数关系式;
(2)若⊙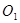 与⊙
与⊙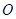 外切,且⊙
外切,且⊙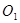 分别与
分别与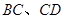
相切于点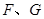 ,求
,求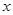 为何值时⊙
为何值时⊙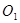 半径为1.
半径为1.
查看答案和解析>>
科目:初中数学 来源: 题型:
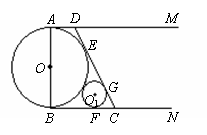
如图所示,⊙![]() 的直径
的直径![]() ,
,![]() 和
和![]() 是它的两条切线,
是它的两条切线,![]() 为射线
为射线![]() 上的动点(不与
上的动点(不与![]() 重合),
重合),![]() 切⊙
切⊙![]() 于
于![]() ,交
,交![]() 于
于![]() ,设
,设![]() .
.
(1)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)若⊙![]() 与⊙
与⊙![]() 外切,且⊙
外切,且⊙![]() 分别与
分别与![]()
相切于点![]() ,求
,求![]() 为何值时⊙
为何值时⊙![]() 半径为1.
半径为1.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com