
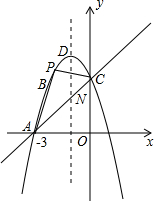
 如图,已知抛物线y=ax2+bx+c过点A(-3,0),B(-2,3),C(0,3),其顶点为D.
如图,已知抛物线y=ax2+bx+c过点A(-3,0),B(-2,3),C(0,3),其顶点为D.分析 (1)根据待定系数法,可得答案;
(2)利用轴对称求最短路径的知识,找到B点关于直线x=1的对称点B′,连接B'D,B'D与直线x=1的交点即是点M的位置,继而求出m的值.
(3)根据平行于y轴的直线上两点间的距离是较大的纵坐标减去较小的纵坐标,可得PE的长,根据三角形的面积,可得二次函数,根据二次函数的性质,可得答案;
(4)设出点E的,分情况讨论,①当点E在线段AC上时,点F在点E上方,②当点E在线段AC(或CA)延长线上时,点F在点E下方,根据平行四边形的性质,可得关于x的方程,继而求出点E的坐标.
解答 解:(1)将A,B,C点的坐标代入解析式,得
$\left\{\begin{array}{l}{9a-3b+c=0}\\{4a-2b+c=3}\\{c=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-1}\\{b=-2}\\{c=3}\end{array}\right.$,
抛物线的解析式为y=-x2-2x+3
(2)配方,得y=-(x+1)2+4,顶点D的坐标为(-1,4)
作B点关于直线x=1的对称点B′,如图1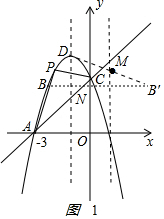 ,
,
则B′(4,3),由(1)得D(-1,4),
可求出直线DB′的函数关系式为y=-$\frac{1}{5}$x+$\frac{19}{5}$,
当M(1,m)在直线DN′上时,MN+MD的值最小,
则m=-$\frac{1}{5}$×1+$\frac{19}{5}$=$\frac{18}{5}$.
(3)作PE⊥x轴交AC于E点,如图2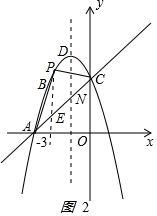 ,
,
AC的解析式为y=x+3,设P(m,-m2-2m+3),E(m,m+3),
PE=-m2-2m+3-(m+3)=-m2-3m
S△APC=$\frac{1}{2}$PE•|xA|=$\frac{1}{2}$(-m2-3m)×3=-$\frac{3}{2}$(m+$\frac{3}{2}$)2+$\frac{27}{8}$,
当m=-$\frac{3}{2}$时,△APC的面积的最大值是$\frac{27}{8}$;
(4)由(1)、(2)得D(-1,4),N(-1,2)
点E在直线AC上,设E(x,x+3),
①当点E在线段AC上时,点F在点E上方,则F(x,-x2-2x+3),
∵EF=DN
∴-x2-2x+3-(x+3)=4-2=2,
解得,x=-2或x=-1(舍去),
则点E的坐标为:(-2,1).
②当点E在线段AC(或CA)延长线上时,点F在点E下方,则F(x,-x2-2x+3),
∵EF=DN,
∴(x+3)-(-x2-2x+3)=2,
解得x=$\frac{-3+\sqrt{17}}{2}$或x=$\frac{-3-\sqrt{17}}{2}$,
即点E的坐标为:($\frac{-3+\sqrt{17}}{2}$,$\frac{3+\sqrt{17}}{2}$)或($\frac{-3-\sqrt{17}}{2}$,$\frac{3-\sqrt{17}}{2}$)
综上可得满足条件的点E为E(-2,1)或:($\frac{-3+\sqrt{17}}{2}$,$\frac{3+\sqrt{17}}{2}$)或($\frac{-3-\sqrt{17}}{2}$,$\frac{3-\sqrt{17}}{2}$).
点评 本题考查了二次函数的综合题,解(1)的关键是待定系数法,解(2)利用轴对称求最短路径;解(3)的关键是利用三角形的面积得出二次函数;解(4)的关键是平行四边形的性质得出关于x的方程,要分类讨论,以防遗漏.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2是4的算术平方根 | B. | $\frac{1}{3}$是$\frac{1}{9}$的一个平方根 | ||
| C. | (-1)2的平方根是-1 | D. | 0的平方根是0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a+c>b+c | B. | a-c<b-c | C. | ac>bc | D. | $\frac{a}{c}$>$\frac{b}{c}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 甲型 | 乙型 | |
| 价格(元/台) | a | b |
| 有效半径(米/台) | 150 | 100 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com