
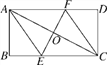
【题目】如图,将矩形ABCD折叠使A,C重合,折痕交BC于E,交AD于F,连接AE,CF,AC.
(1)求证:四边形AECF为菱形;
(2)若AB=4,BC=8,①求菱形AECF的边长;②求折痕EF的长.
【答案】(1)证明见解析;(2)①5;②2![]() .
.
【解析】试题分析:(1)根据折叠的性质得OA=OC,EF⊥AC,EA=EC,再利用AD∥AC,得到∠FAC=∠ECA,则可根据“ASA”判断△AOF≌△COE,得到OF=OE,加上OA=OC,AC⊥EF,于是可根据菱形的判定方法得到四边形AECF为菱形;
(2)①设菱形的边长为x,则BE=BCCE=8x,AE=x,在Rt△ABE中,根据勾股定理得![]() 然后解方程即可得到菱形的边长;
然后解方程即可得到菱形的边长;
②先在Rt△ABC中,利用勾股定理计算出![]() 则
则![]() 然后在Rt△AOE中,利用勾股定理计算出
然后在Rt△AOE中,利用勾股定理计算出![]()
试题解析:证明:(1)∵矩形ABCD折叠使A,C重合,折痕为EF,
∴OA=OC,EF⊥AC,EA=EC,
∵AD∥AC,
∴∠FAC=∠ECA,
在△AOF和△COE中,

∴△AOF≌△COE,
∴OF=OE,
∵OA=OC,AC⊥EF,
∴四边形AECF为菱形;
(2)①设菱形的边长为x,则BE=BCCE=8x,AE=x,
在Rt△ABE中,∵![]()
∴![]() 解得x=5,
解得x=5,
即菱形的边长为5;
②在Rt△ABC中, ![]()
∴![]()
在Rt△AOE中,AE=5,
![]()
∴![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】梅岭中学为了解“课程选修”的情况,对报名参加“艺术欣赏”,“科技制作”,“数学思维”,“阅读写作”这四个选修项目的学生(每人限报一课)进行抽样调查,下面是根据收集的数据绘制的不完整的统计图,请根据图中提供的信息,解答下面的问题:
(1)此次共调查了______名学生,扇形统计图中“艺术欣赏”部分的圆心角是______度;
(2)请把这个条形统计图补充完整;
(3)现该校共有800名学生报名参加这四个选修项目,请你估计其中有多少名学生选修 “科技制作”项目.

查看答案和解析>>
科目:初中数学 来源: 题型:
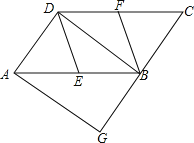
【题目】如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,过A点作AG∥DB,交CB的延长线于点G.
(1)求证:DE∥BF;
(2)若∠G=90,求证:四边形DEBF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
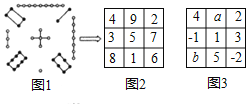
【题目】(阅读材料)“九宫图”源于我国古代夏禹时期的“洛书”![]() 图1所示
图1所示![]() ,是世界上最早的矩阵,又称“幻方”,用今天的数学符号翻译出来,“洛书”就是一个三阶“幻方”
,是世界上最早的矩阵,又称“幻方”,用今天的数学符号翻译出来,“洛书”就是一个三阶“幻方”![]() 图2所示
图2所示![]() .
.
(规律总结)观察图1、图2,根据“九宫图”中各数字之间的关系,我们可以总结出“幻方”需要满足的条件是______;若图3,是一个“幻方”,则![]() ______.
______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F. 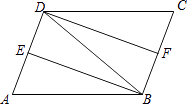
(1)求证:△ABE≌△CDF;
(2)若AB=DB,猜想:四边形DFBE是什么特殊的四边形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知代数式![]() ,当
,当![]() 时,该代数式的值为-1.
时,该代数式的值为-1.
(1)求![]() 的值。
的值。
(2)已知当![]() 时,该代数式的值为-1,求
时,该代数式的值为-1,求![]() 的值。
的值。
(3)已知当![]() 时,该代数式的值为9,试求当
时,该代数式的值为9,试求当![]() 时该代数式的值。
时该代数式的值。
(4)在第(3)小题已知条件下,若有![]() 成立,试比较
成立,试比较![]() 与
与![]() 的大小。
的大小。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知n边形的内角和θ=(n-2)×180°.
(1)甲同学说,θ能取360°;而乙同学说,θ也能取630°.甲、乙的说法对吗?若对,求出边数n.若不对,说明理由;
(2)若n边形变为(n+x)边形,发现内角和增加了360°,用列方程的方法确定x.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,制作某金属工具先将材料煅烧6分钟温度升到800℃,再停止煅烧进行锻造,8分钟温度降为600℃;煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时温度y(℃)与时间x(min)成反比例函数关系;该材料初始温度是32℃. 
(1)分别求出材料煅烧和锻造时y与x的函数关系式;
(2)根据工艺要求,当材料温度低于480℃时,须停止操作,那么锻造的操作时间有多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李对初三(1)班全体同学的业余兴趣爱好(第一爱好)进行了一次调查,她根据采集到的数据,绘制了下面的图1和图2.

请你根据图中提供的信息,解答下列问题:
(1)初三(1)班共有学生________人;
(2)在图1中,将“书画”部分的图形补充完整;
(3)在图2中,“球类”部分所对应的圆心角的度数________度;爱好“音乐”的人数占本班学生数的百分数是________;爱好“书画”的人数占本班学生数的百分数是________;“其它”的人数占本班学生数的百分数是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com