Question

【题目】已知:三角形ABC中,∠A=90°,AB=AC,D为BC的中点.

(1)如图,E、F分别是AB、AC上的点,且BE=AF,求证:△DEF为等腰直角三角形.

(2)若E、F分别为AB,CA延长线上的点,仍有BE=AF,其他条件不变,那么,△DEF是否仍为等腰直角三角形?画出图形,写出结论不证明.

Answer 1

【答案】（1）见解析；（2）见解析

【解析】

(1)先连接AD，构造全等三角形：△BED和△AFD．AD是等腰直角三角形ABC底边上的中线，所以有∠CAD=∠BAD=45°，AD=BD=CD，而∠B=∠C=45°，所以∠B=∠DAF，再加上BE=AF，AD=BD，可证出：△BED≌△AFD，从而得出DE=DF，∠BDE=∠ADF，从而得出∠EDF=90°，即△DEF是等腰直角三角形；

(2)根据题意画出图形,连接AD,构造△DAF≌△DBE.得出FD=ED ,∠FDA=∠EDB,再算出∠EDF=90°,即可得出△DEF是等腰直角三角形.

解：（1）连结AD ,

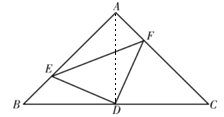
∵AB=AC ,∠BAC=90° ,D为BC中点 ,

∴AD⊥BC ,BD=AD ,

∴∠B=∠BAD=∠DAC=45°,

又∵BE=AF ,

∴△BDE≌△ADF（SAS）,

∴ED=FD ,∠BDE=∠ADF,

∴∠EDF=∠EDA+∠ADF=∠EDA+∠BDE=∠BDA=90°,

∴△DEF为等腰直角三角形.

（2）连结AD

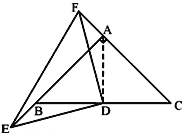
∵AB=AC ,∠BAC=90° ,D为BC中点 ,

∴AD=BD ,AD⊥BC ,

∴∠DAC=∠ABD=45° ,

∴∠DAF=∠DBE=135°,

又∵AF=BE ,

∴△DAF≌△DBE（SAS）,

∴FD=ED ,∠FDA=∠EDB,

∴∠EDF=∠EDB+∠FDB=∠FDA+∠FDB=∠ADB=90°.

∴△DEF为等腰直角三角形.