
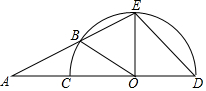
 如图,CD是半圆的直径,O为圆心,E是半圆上一点,且∠EOD=93°,A是DC延长线上一点,AE与半圆相交于点B.若AB=OC,则∠EAD=31°,∠EOB=56°.
如图,CD是半圆的直径,O为圆心,E是半圆上一点,且∠EOD=93°,A是DC延长线上一点,AE与半圆相交于点B.若AB=OC,则∠EAD=31°,∠EOB=56°. 分析 设∠A=x,由AB=OC,得到∠BOA=x,根据三角形外角性质得到∠EBO=2x,而OB=OE,得∠AEO=2x,则x+2x=93°,得到x=31°,再根据三角形的内角和定理得∠EOB=180°-4x=180°-124°=56°.
解答 解:设∠A=x,
∵AB=OC,
∴∠BOA=x,
∴∠EBO=2x,
而OB=OE,
∴∠AEO=2x,
∴∠EOD=∠A+∠AEO,
而∠EOD=93°,
∴x+2x=93°,
∴x=31°,
∴∠EOB=180°-4x=180°-124°=56°.
故答案为:31°;56°.
点评 本题考查了在同圆或等圆中,如果两个圆心角以及它们对应的两条弧、两条弦中有一组量相等,则另外两组量也对应相等.也考查了等腰三角形的性质和三角形内角和定理以及外角性质.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 将下列各式分解因式:
将下列各式分解因式:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com