
【题目】已知抛物线y=ax2+bx+c的顶点为D(﹣1,2),其部分图象如图所示,给出下列四个结论: ①a<0; ②b2﹣4ac>0;③2a﹣b=0;④若点P(x0 , y0)在抛物线上,则ax02+bx0+c≤a﹣b+c.其中结论正确的是( )
A.1个
B.2个
C.3个
D.4个
【答案】D
【解析】解:∵抛物线开口向下, ∴a<0,所以①正确;
∵抛物线与x轴有2个交点,
∴△=b2﹣4ac>0,所以②正确;
∵抛物线y=ax2+bx+c的顶点为D(﹣1,2),
∴抛物线的对称轴为直线x=﹣ ![]() =﹣1,
=﹣1,
∴b=2a,即2a﹣b=0,所以③正确;
∵抛物线y=ax2+bx+c的顶点为D(﹣1,2),
∴x=﹣1时,y有最大值2,
∴点P(x0 , y0)在抛物线上,则ax02+bx0+c≤a﹣b+c,所以④正确.
故选D.
【考点精析】本题主要考查了二次函数图象以及系数a、b、c的关系的相关知识点,需要掌握二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c)才能正确解答此题.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,∠A=90°,AB=4,AC=3,M是AB上的动点(不与A,B重合),过M点作MN∥BC交AC于点N.以MN为直径作⊙O,并在⊙O内作内接矩形AMPN.令AM=x.
(1)用含x的代数式表示△MNP的面积S;
(2)当x为何值时,⊙O与直线BC相切;
(3)在动点M的运动过程中,记△MNP与梯形BCNM重合的面积为y,试求y关于x的函数表达式,并求x为何值时,y的值最大,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC与△A′B′C′中,有下列条件:(1) ![]() ,(2)
,(2) ![]() ;(3)∠A=∠A′;(4)∠C=∠C′,如果从中任取两个条件组成一组,那么能判断△ABC∽△A′B′C′的共有( )
;(3)∠A=∠A′;(4)∠C=∠C′,如果从中任取两个条件组成一组,那么能判断△ABC∽△A′B′C′的共有( )
A.1组
B.2组
C.3组
D.4组
查看答案和解析>>
科目:初中数学 来源: 题型:
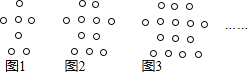
【题目】下列图形都是由同样大小的空心圆圈按照一定规律所组成的,其中图![]() 中一共有7个空心圆圈;图
中一共有7个空心圆圈;图![]() 中一共有11个空心圆圈;图
中一共有11个空心圆圈;图![]() 中一共有15个空心圆圈;
中一共有15个空心圆圈;![]()
![]() 图
图![]() 一共应有______个空心圆圈.
一共应有______个空心圆圈.
![]() 按此规律排列下去,猜想图
按此规律排列下去,猜想图![]() 中一共有多少个空心圆圈?用含n的代数式表示
中一共有多少个空心圆圈?用含n的代数式表示![]() 不用说理
不用说理![]() .
.
![]() 是否存在图
是否存在图![]() 中一共有2018个空心圆圈?若存在,求出x的值;若不存在,请说明理由.
中一共有2018个空心圆圈?若存在,求出x的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A( ![]() ,
, ![]() )和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
(1)求抛物线的解析式;
(2)是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;
(3)求△PAC为直角三角形时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
小明在一本课外读物上看到一道有意思的数学题:例1、解不等式:![]() ,根据绝对值的几何意义,到原点距离小于1的点在数轴上集中在-1和+1之间,如图:
,根据绝对值的几何意义,到原点距离小于1的点在数轴上集中在-1和+1之间,如图:
![]()
所以,该不等式的解集为-1<x<1.
因此,不等式![]() 的解集为x<-1或x>1.
的解集为x<-1或x>1.
根据以上方法小明继续探究:例2:求不等式:![]() 的解集,即求到原点的距离大于2小于5的点的集合就集中在这样的区域内,如图:
的解集,即求到原点的距离大于2小于5的点的集合就集中在这样的区域内,如图:
![]()
所以,不等式![]() 的解集为-5<x<-2或2<x<5.
的解集为-5<x<-2或2<x<5.
仿照小明的做法解决下面问题:
(1)不等式![]() 的解集为____________.
的解集为____________.
(2)不等式![]() 的解集是____________.
的解集是____________.
(3)求不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从热气球C处测得地面A、B两点的俯角分别是30°、45°,如果此时热气球C处的高度CD为100米,点A、D、B在同一直线上,则AB两点的距离是( )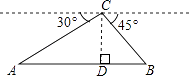
A.200米
B.200 ![]() 米
米
C.220 ![]() 米
米
D.100( ![]() +1)米
+1)米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com