
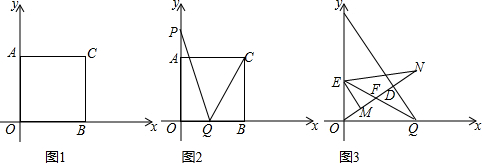
���� ��1�������÷Ǹ��Խ����������a��b�����ó���A��B���꣬���ô�ֱȷ������C���ꣻ
��2�����жϳ�OACB�������Σ��ó�AC=BC�������жϳ���BCQ�ա�ACP���ó�PC=QC����ACP=��BCQ�����ɵó�������PCQ�ǵ���ֱ�������Σ����ɣ�
��3�����ý�ƽ���ߵ����ʵó�EG=OE�����жϳ���EOQ�ա�EGQ���ó���OEQ=��GEQ�������жϳ��ı���OEGF�����Σ��ı���EFNG��ƽ���ı��Σ��ó�EH=$\frac{1}{2}$EN��FH=$\frac{1}{2}$FG������жϳ���EFM�ա�EFH�����Ƶ������ۣ�
��� �⣺��1����$\sqrt{a+b-4}$+|a-2b+2|=0��
��a+b-4=0��a-2b+2=0��
��a=2��b=2��
��A��0��a����B��b��0����
��A��0��2����B��2��0����
�ߵ�A�͵�B��y���x��Ĵ��ߣ����ڵ�C��
��C��2��2����
��2����CQP�Ĵ�С�������仯���Ƕ�ֵ45�㣮
���ɣ���ͼ2��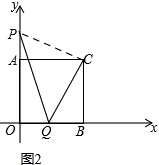
����PC��
�ߵ�A�͵�B��y���x��Ĵ��ߣ����ڵ�C��
���OBC=��OAC=90�㣬
�ߡ�AOB=90�㣬
���OBC=��OAC=��AOB=90�㣬
���ı���OACB�Ǿ��Σ�
�ɣ�1��֪��OA=OB��
�����OACB��������
��BC=AC��
���˶�֪��BQ=AP��
�ڡ�BCQ�͡�ACP�У�$\left\{\begin{array}{l}{BC=AC}\\{��QBC=��APC}\\{BQ=AP}\end{array}\right.$��
���BCQ�ա�ACP��
��CQ=CP����BCQ=��ACP��
�ߡ�ACQ+��BCQ=90�㣬
���PCQ=��ACQ+��ACP=��ACQ+��BCQ=90�㣬
���PCQ�ǵ���ֱ�������Σ�
���PQC=45�㣬
���CQP�Ĵ�С�������仯���Ƕ�ֵ45�㣮
��3����$\frac{EN}{EM}$Ϊ��ֵ��Ϊ$\frac{1}{2}$��
���ɣ���ͼ3��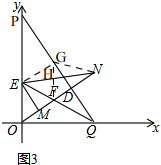
����E��EG��PQ������GN��GF��
��OD��PQ��
��ON��EG��
���GEF=��OFE��
��QEƽ�֡�OQP��EG��PQ��EO��OQ��
��EG=EO��
�ڡ�OQE�͡�GQE�У�$\left\{\begin{array}{l}{EO=EG}\\{��EOQ=��EGQ=90��}\\{EQ=EQ}\end{array}\right.$��
���OQE�ա�GQE��
���OEF=��GEF��
�ߡ�GEF=��OFE��
���OEF=��OFE��
��OE=OF��
��EG=OF��
��EG��OD��
���ı���OEGF��ƽ���ı��Σ�
��OE=OF��
��ƽ���ı���OEGF�����Σ�
��OF=FG����OFE=��GFE
��ON=2OF=OF+FN��
��EG=FN��
��EG��FN��
���ı���EFNG��ƽ���ı��Σ�
��EH=NH=$\frac{1}{2}$EN��FH=$\frac{1}{2}$FG��
��M��OF�е㣬
��FM=$\frac{1}{2}$OF��
��FM=FH��
�ڡ�EFM�͡�EFH�У�$\left\{\begin{array}{l}{FM=FH}\\{��EFM=��EFH}\\{EF=EF}\end{array}\right.$��
���EFM�ա�EFH��
��EM=EH��
��EM=$\frac{1}{2}$EN��
���$\frac{EN}{EM}$=$\frac{1}{2}$���Ƕ�ֵ��
���� �������������ۺ��⣬��Ҫ�����������ε����ʺ��ж�������ֱ�������ε��ж������ʣ�ȫ�������ε����ʺ��ж���ƽ���ı��Σ����ε��ж������ʣ���ƽ���ߵ����ʣ��Ȿ��ĸ����ǹ���ȫ�������Σ���һ���п������⣮


 ��ǰ����ϵ�д�
��ǰ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
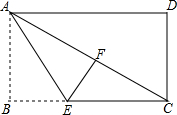
 ��ͼ������ABCD�У�CEƽ�֡�BCD��AD��F��AE��CE��E����BE��AD��N����BD��CE��M����CE=CB�������н��ۣ��١�AEF�ա�CDF����NΪBE�Ļƽ�ָ�㣻��S��MBC=��3+2$\sqrt{2}$��S��NEA����BD=$\sqrt{2}$BE��������ȷ���۸����ǣ�������
��ͼ������ABCD�У�CEƽ�֡�BCD��AD��F��AE��CE��E����BE��AD��N����BD��CE��M����CE=CB�������н��ۣ��١�AEF�ա�CDF����NΪBE�Ļƽ�ָ�㣻��S��MBC=��3+2$\sqrt{2}$��S��NEA����BD=$\sqrt{2}$BE��������ȷ���۸����ǣ�������| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪�����ߵĶ���ΪA��1��4������������y�ύ�ڵ�B��0��3������x�ύ��C��D���㣮��P��x���ϵ�һ�����㣮
��ͼ����֪�����ߵĶ���ΪA��1��4������������y�ύ�ڵ�B��0��3������x�ύ��C��D���㣮��P��x���ϵ�һ�����㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��x-1��=20 | B�� | $\frac{x��x-1��}{2}=20$ | C�� | x��x+1��=20 | D�� | $\frac{x��x+1��}{2}=20$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����ֱ�� | B�� | ���ǰ�Բ | ||
| C�� | ��Բ��Բ����Ļ� | D�� | ֱ����Բ������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3x2-2xy-5y2=0 | B�� | x��x-3��=x2+5 | C�� | x-$\frac{2}{x}$=8 | D�� | x��x-2��=3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ���ھ���ֽƬABCD�У�AB=6��AD=8���۵���ֽƬ��ʹ��AB�����ڶԽ���AC�ϣ���B���ڵ�F�����ۺ�ΪAE�����߶�EF�ij�Ϊ��������
��ͼ���ھ���ֽƬABCD�У�AB=6��AD=8���۵���ֽƬ��ʹ��AB�����ڶԽ���AC�ϣ���B���ڵ�F�����ۺ�ΪAE�����߶�EF�ij�Ϊ��������| A�� | 3 | B�� | 4 | C�� | 5 | D�� | 6 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com