
����Ŀ�����������⣩������ѧ��С��������ҵʱ����������һ����Ŀ��
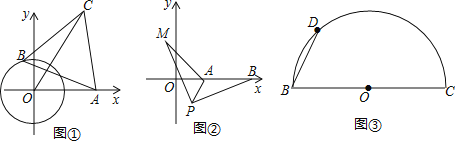
��ͼ�٣���OΪ����ԭ�㣬��O�İ뾶Ϊ1����A��2��0��������B�ڡ�O�ϣ�����AB�����ȱߡ�ABC��A��B��CΪ˳ʱ��˳����OC�����ֵ
��������⣩С��������εij�����̽�������ڵõ�����˼·����ͼ���У�����OB����OBΪ����OB��������ȱ�������BOE������AE��
��1�������ҳ�ͼ����OC��ȵ��߶Σ���˵�����ɣ�
��2�����߶�OC�����ֵ��
��������ã�
��3����ͼ�ڣ���ƽ��ֱ������ϵ�У���A������Ϊ��2��0������B������Ϊ��5��0������PΪ�߶�AB��һ���㣬��PA��2��PM��PB����BPM��90�㣬���߶�AM�������ֵ����ʱ��P�����꣮
��Ǩ����չ��
��4����ͼ�ۣ�BC��4![]() ����D����BCΪֱ���İ�Բ�ϲ�ͬ��B��C��һ�����㣬��BDΪ�����ȱߡ�ABD����ֱ��д��AC����ֵ��
����D����BCΪֱ���İ�Բ�ϲ�ͬ��B��C��һ�����㣬��BDΪ�����ȱߡ�ABD����ֱ��д��AC����ֵ��
���𰸡���1�����ۣ�OC��AE�����ɼ���������2��OC�����ֵΪ3����3�����ֵΪ2![]() +3��P��2��
+3��P��2��![]() ��
��![]() ������4��AC�����ֵΪ2
������4��AC�����ֵΪ2![]() +2
+2![]() �� 2
�� 2![]() ��2
��2![]() ��
��
��������
��1�����ۣ�![]() ��ֻҪ֤��
��ֻҪ֤��![]() ���ɣ�
���ɣ�
��2�����������ε����߹�ϵ���ɽ�����⣻
��3������![]() ����
����![]() ���ŵ�
���ŵ�![]() ˳ʱ����ת
˳ʱ����ת![]() �õ�
�õ�![]() ������
������![]() ���õ�
���õ�![]() �ǵ���ֱ�������Σ�����ȫ�������ε����ʵõ�
�ǵ���ֱ�������Σ�����ȫ�������ε����ʵõ�![]() ��
��![]() �����ݵ�
�����ݵ�![]() ���߶�
���߶�![]() ���ӳ���ʱ���߶�
���ӳ���ʱ���߶�![]() ȡ�����ֵ�����ɵõ����ֵΪ
ȡ�����ֵ�����ɵõ����ֵΪ![]() ����
����![]() ��
��![]() ����
����![]() �����ݵ���ֱ�������ε����ʣ����ɵõ����ۣ�
�����ݵ���ֱ�������ε����ʣ����ɵõ����ۣ�
��4����ͼ4�У���![]() Ϊ�����ȱ�������
Ϊ�����ȱ�������![]() ����
����![]() ���Ƴ�
���Ƴ�![]() ���Ƴ�����
���Ƴ�����![]() �����ֵ��ֻҪ���
�����ֵ��ֻҪ���![]() �����ֵ���ɣ���
�����ֵ���ɣ���![]() ��ֵ��
��ֵ��![]() ���Ƴ���
���Ƴ���![]() ����
����![]() Ϊֱ����
Ϊֱ����![]() ���˶�����ͼ���֪������
���˶�����ͼ���֪������![]() ��
��![]() �Ϸ���
�Ϸ���![]() ʱ��
ʱ��![]() ��ֵ���.
��ֵ���.
��1����ͼ���У����ۣ�OC��AE��
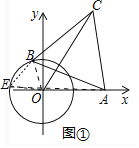
���ɣ��ߡ�ABC����BOE���ǵȱ������Σ�
��BC��BA��BO��BE����CBA����OBE��60�㣬
���CBO����ABE��
���CBO�ա�ABE��
��OC��AE��
��2���ڡ�AOE�У�AE��OE+OA��
�൱E��O��A���ߣ�
��AE�����ֵΪ3��
��OC�����ֵΪ3��
��3����ͼ1������BM��
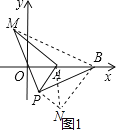
�߽���APM���ŵ�P˳ʱ����ת90��õ���PBN������AN�����APN�ǵ���ֱ�������Σ�
��PN��PA��2��BN��AM��
��A��������2��0������B��������5��0����
��OA��2��OB��5��
��AB��3��
���߶�AM�������ֵ���߶�BN�������ֵ��
�൱N���߶�BA���ӳ���ʱ���߶�BNȡ�����ֵ����ͼ2�У�
���ֵ��AB+AN��
��AN��![]() AP��2
AP��2![]() ��
��
�����ֵΪ2![]() +3��
+3��
��ͼ2����P��PE��x����E��

�ߡ�APN�ǵ���ֱ�������Σ�
��PE��AE��![]() ��
��
��OE��BO��AB��AE��5��3��![]() ��2��
��2��![]() ��
��
��P��2��![]() ��
��![]() ����
����
��4����ͼ4�У���BCΪ�����ȱ������Ρ�BCM��

�ߡ�ABD����CBM��60�㣬
���ABC����DBM����AB��DB��BC��BM��
���ABC�ա�DBM��
��AC��MD��
������AC�����ֵ��ֻҪ���DM�����ֵ���ɣ�
��BC��4![]() ����ֵ����BDC��90�㣬
����ֵ����BDC��90�㣬
���D����BCΪֱ���ġ�O���˶���
��ͼ���֪������D��BC�Ϸ���DM��BCʱ��DM��ֵ������ֵ��2![]() +2
+2![]() ��
��
��AC�����ֵΪ2![]() +2
+2![]() ��
��
����A���߶�BD���Ҳ�ʱ��ͬ���ɵ�AC����СֵΪ2![]() ��2
��2![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����豱�����㳡����ͣ������5������ڣ�ÿ���糿6�㿪ʼ����ͣ���Ҵ�ʱ��λ������Ϊ75%����ÿ������ڵij������������ٳ��������£��������2�����ں�3�����ڣ�8Сʱ����ǡ��ͣ�����������3�����ں�2�����ڣ�2Сʱ����ǡ��ͣ����2019��Ԫ�����ڼ䣬�����̳��������࣬�糿6��ʱ�ij�λ�����ʱ�Ϊ60%������Ϊ������죬ֻ�ܿ���2�����ں�1�����ڣ�����糿6�㿪ʼ����________Сʱ����ǡ��ͣ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
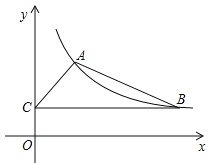
����Ŀ����ͼ��ij����������ͼ���һ֧������A��2��3���͵�B����B�ڵ�A���Ҳࣩ����BC��y�ᣬ����Ϊ��C������AB��AC��
��1����÷����������Ľ���ʽ��
��2������ABC�����Ϊ6����ֱ��AB�ı���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ�������߳�Ϊ4cm��������ֽƬABCD��EF�۵�(��E��F�ֱ��ڱ�AB��CD��)��ʹ��B����AD���ϵĵ� M������C���ڵ�N����MN��CD���ڵ�P�� ����EP��
����ͼ������MΪAD�ߵ��е㣬�١�AEM���ܳ�=_________cm������֤��EP=AE+DP��
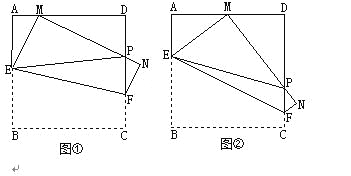
���������M��AD����ȡ�����е�λ��(��M����A��D�غ�)����PDM���ܳ��Ƿ����仯?��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABΪ��O��ֱ����CΪ��O��һ�㣬��CAB�Ľ�ƽ����AD����O�ڵ�D������D��DE��AC��AC���ӳ����ڵ�E��
��1����֤��DE�ǡ�O�����ߣ�
��2������CAB=60�㣬DE=3![]() ����AC�ij���
����AC�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������С������ֱ����һ��������ֱ�ߵĴ��ߡ��ij߹���ͼ����.
��֪��ֱ��l��ֱ��l��һ��P.
������ֱ��PQ��ʹ��PQ��l.
��������ͼ��
����ֱ��l�����ȡһ��K���Ե�PΪԲ�ģ�PK��Ϊ�뾶��������ֱ��l�ڵ�A��B��
�ڷֱ��Ե�A��BΪԲ�ģ�����![]() AB��ͬ����Ϊ�뾶�������������ڵ�Q(��P�㲻�غ�)��
AB��ͬ����Ϊ�뾶�������������ڵ�Q(��P�㲻�غ�)��
����ֱ��PQ����ֱ��PQ������������ֱ��.
����С����Ƶij߹���ͼ���̣�
(1)ʹ��ֱ�ߺ�Բ�棬��ȫͼ�Σ�(������ͼ�ۼ�)
(2)��������֤��.
֤������PA= ��QA= ,
��PQ��l( )(������������).

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
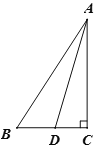
����Ŀ����ͼ��Rt�� ABC�У���ACB=90�㣬ADƽ����BAC�� ��AD�Ĵ�ֱƽ����EF��AD�ڵ�E����BC���ӳ����ڵ�F����AB�ڵ�G����AC�ڵ�H��
(1)�����ⲹȫͼ�Σ�
(2)��֤����BAD=��BFG��
(3)�Բ���AB��FB��FD֮���������ϵ������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���涨ѧ��ÿ�컧�������ʱ�䲻����1Сʱ.Ϊ�˽�ѧ���μӻ����������������Բ���ѧ��ÿ��μӻ����������ʱ�����������������飬�������������Ƴ����µ�ͳ�Ʊ�����������.
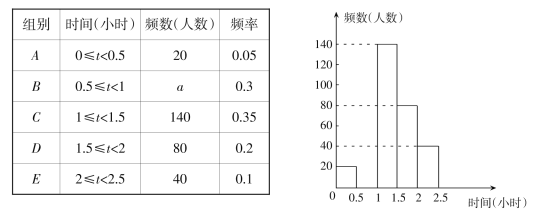
�����ͼ���е���Ϣ������������⣺
��1��д������a��ֵ����Ƶ���ֲ�ֱ��ͼ��ȫ��
��2������8000��ѧ���У�ÿ�컧���������ʱ�䲻��1Сʱ��ѧ����Լ�ж�������
��3�����Ӳμӻ��������ʱ�����3��������1��Ů���������ȡ���������û���״ͼ���б�����ǡ�ó鵽1��������1��Ů���ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����һ����������һ�ŵȱ�������(��ABC)ֽƬ���ó���Գ�ͼ�Σ�CD��AB,����ΪD����Բ(������)��Բ�����D�غϣ���ʱ����ö���C����������ߵ�ľ���CE��2cm������������DC����ƽ��1cm����Բ(������)ǡ���ABC�ı�AC��BC���У���ͼ2,��AB�ij�Ϊ__________cm.
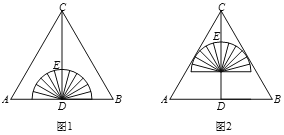
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com