Question

5．如图1，Rt△ABC中，∠ACB=Rt∠，AC=8，BC=6，点D为AB的中点，动点P从点A出发，沿AC方向以每秒1个单位的速度向终点C运动，同时动点Q从点C出发，以每秒2个单位的速度先沿CB方向运动到点B，再沿BA方向向终点A运动，以DP，DQ为邻边构造?PEQD，设点P运动的时间为t秒．
（1）当t=2时，求PD的长；
（2）如图2，当点Q运动至点B时，连结DE，求证：DE∥AP．
（3）如图3，连结CD．
①当点E恰好落在△ACD的边上时，求所有满足要求的t值；
②记运动过程中?PEQD的面积为S，?PEQD与△ACD的重叠部分面积为S₁，当$\frac{{S}_{1}}{S}$＜$\frac{1}{3}$时，请直接写出t的取值范围是$\frac{72}{25}$＜t＜$\frac{56}{17}$．．

Answer 1

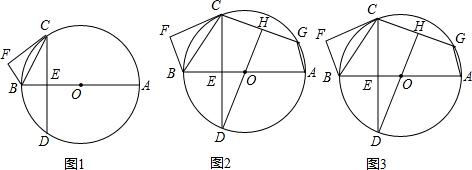
分析 （1）如图1中，作DF⊥CA于F，求出DF、PF，利用勾股定理即可解决问题．
（2）只要证明四边形APED是平行四边形即可．
（3）①分三种情形Ⅰ．当点E在CA上时，Ⅱ．当点E在CD上，且点Q在CB上时 （如图4所示），Ⅲ．当点E在CD上，且点Q在AB上时（如图5所示），过点E作EF⊥CA于点F，分别计算即可．
②Ⅰ、如图6中，PE交CD于E′，作E′G′⊥AC于G′，EG⊥AC于G．当△PDE′的面积等于平行四边形PEDQD的面积 的$\frac{1}{3}$时，求出t的值．Ⅱ、如图7中，当点Q在AB上时，PE交CD于E′，作E′G′⊥AC于G′．当△PDE′的面积等于平行四边形PEDQD的面积 的$\frac{1}{3}$时，求出t的值．由此即可解决问题．

解答 解：（1）如图1中，作DF⊥CA于F，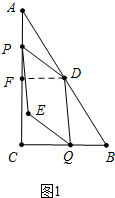

当t=2时，AP=2，DF=AD•sinA=5×$\frac{3}{5}$=3，
∵AF=AD•cosA=5×$\frac{4}{5}$=4，
∴PF=4-2=2，
∴PD=$\sqrt{D{F}^{2}+P{F}^{2}}$=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$．

（2）如图2中，

在平行四边形PEQD中，
∵PE∥DQ，
∴PE∥AD，
∵AD=DQ．PE=DQ，
∴PE=AD，
∴四边形APED是平行四边形，
∴DE∥AP．

（3）①分三种情况讨论：
Ⅰ．当点E在CA上时，
DQ⊥CB（如图3所示），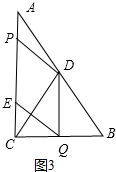

∵∠ACB=Rt∠，CD 是中线，∴CD=BD，∴CQ=$\frac{1}{2}$CB=3
即：t=$\frac{3}{2}$

Ⅱ．当点E在CD上，且点Q在CB上时 （如图4所示），

过点E作EG⊥CA于点G，过点D作DH⊥CB于点H，
易证Rt△PGE≌Rt△DHQ，∴PG=DH=4，
∴CG=4-t，GE=HQ=CQ-CH=2t-3，
∵CD=AD，∴∠DCA=∠DAC
∴在Rt△CEG中，tan∠ECG=$\frac{GE}{CG}$=$\frac{2t-3}{4-t}$=$\frac{3}{4}$，∴t=$\frac{24}{11}$
Ⅲ．当点E在CD上，且点Q在AB上时（如图5所示），过点E作EF⊥CA于点F，

∵CD=AD，∴∠CAD=∠ACD．
∵PE∥AD，∴∠CPE=∠CAD=∠ACD，∴PE=CE，
∴PF=$\frac{1}{2}$PC=$\frac{8-t}{2}$，PE=DQ=11-2t，
∴在Rt△PEF中，cos∠EPF=$\frac{PF}{PE}$=$\frac{\frac{8-T}{2}}{11-2t}$=$\frac{4}{5}$
∴t=$\frac{48}{11}$
综上所述，满足要求的t的值为$\frac{3}{2}$或$\frac{24}{11}$或$\frac{48}{11}$．

②如图6中，PE交CD于E′，作E′G′⊥AC于G′，EG⊥AC于G．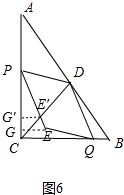

当△PDE′的面积等于平行四边形PEDQD的面积 的$\frac{1}{3}$时，PE′：EE′=2：1，
由（Ⅱ）可知CG=4-t，GE=2t-3，
∴PG=8-t-（4-t）=4，
∵E′G′∥EG，
∴$\frac{PG′}{PG}$=$\frac{E′G′}{EG}$=$\frac{PE′}{PE}$=$\frac{2}{3}$，
∴PG′=$\frac{8}{3}$，E′G′=$\frac{2}{3}$（2t-3），CG′=8-t-$\frac{8}{3}$=$\frac{16}{3}$-t，
∵tan∠ECG=$\frac{E′G′}{CG′}$=$\frac{\frac{2}{3}（2t-3）}{\frac{16}{3}-t}=\frac{3}{4}$，
解得t=$\frac{72}{25}$．
如图7中，当点Q在AB上时，PE交CD于E′，作E′G′⊥AC于G′．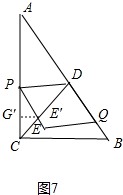

∵△PDE′的面积等于平行四边形PEDQD的面积 的$\frac{1}{3}$，
∴PE′：EE′=2：1，
由Ⅲ可知，PG′=$\frac{1}{2}$PC=4-$\frac{1}{2}$t，PE′=$\frac{2}{3}$DQ=$\frac{2}{3}$（11-2t），
∵cos∠E′PG′=$\frac{PG′}{PE′}$=$\frac{4}{5}$，
∴$\frac{4-\frac{1}{2}t}{\frac{2}{3}（11-2t）}=\frac{4}{5}$，
解得t=$\frac{56}{17}$，
综上所述，当$\frac{{S}_{1}}{S}$＜$\frac{1}{3}$时，请直接写出t的取值范围是$\frac{72}{25}$＜t＜$\frac{56}{17}$．

点评 本题考查四边形综合题、平行四边形的判定和性质、勾股定理、锐角三角函数等知识，解题的关键是灵活运用这些知识解决问题，学会分类讨论，学会取特殊值解决实际问题，属于中考压轴题．