
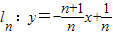 (n是正整数).当n=1时,直线l1:y=-2x+1与 x轴和y轴分别交于点A1和B1,设△A1OB1(O是平面直角坐标系的原点)的面积为s1;当n=2时,直线
(n是正整数).当n=1时,直线l1:y=-2x+1与 x轴和y轴分别交于点A1和B1,设△A1OB1(O是平面直角坐标系的原点)的面积为s1;当n=2时,直线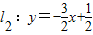 与x轴和y轴分别交于点A2和B2,设△A2OB2的面积为s2,…,依此类推,直线ln与x轴和y轴分别交于点An和Bn,设△AnOBn的面积为Sn.
与x轴和y轴分别交于点A2和B2,设△A2OB2的面积为s2,…,依此类推,直线ln与x轴和y轴分别交于点An和Bn,设△AnOBn的面积为Sn. ×1×
×1× =
= ×(1-
×(1- ),同理求出S2=
),同理求出S2= ×(
×( -
- ),S3=
),S3= (
( -
- ),…S2009=
),…S2009= ×(
×(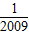 -
-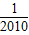 ),代入S1+S2+S3+…+S2009求出即可.
),代入S1+S2+S3+…+S2009求出即可. ,
, ×1×
×1× =
= ,
, .
. ×1×
×1× =
= ×(1-
×(1- ),
), ×
× ×
× =
= ×(
×( -
- ),
), (
( -
- ),
), ×(
×(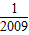 -
-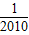 ),
), ×(1-
×(1- +
+ -
- +
+ -
- +…+
+…+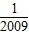 -
- ),
), ×(1-
×(1-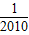 )=
)=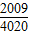 ,
,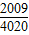 .
.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
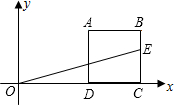 如图,正方形ABCD被直线OE分成面积相等的两部分,已知线段OD、AD的长都是正整数,
如图,正方形ABCD被直线OE分成面积相等的两部分,已知线段OD、AD的长都是正整数,| CE |
| BE |
| A、324 | B、331 |
| C、354 | D、361 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (n是正整数).当n=1时,直线l1:y=-2x+1与 x轴和y轴分别交于点A1和B1,设△A1OB1(O是平面直角坐标系的原点)的面积为s1;当n=2时,直线
(n是正整数).当n=1时,直线l1:y=-2x+1与 x轴和y轴分别交于点A1和B1,设△A1OB1(O是平面直角坐标系的原点)的面积为s1;当n=2时,直线 与x轴和y轴分别交于点A2和B2,设△A2OB2的面积为s2,…,依此类推,直线ln与x轴和y轴分别交于点An和Bn,设△AnOBn的面积为Sn.
与x轴和y轴分别交于点A2和B2,设△A2OB2的面积为s2,…,依此类推,直线ln与x轴和y轴分别交于点An和Bn,设△AnOBn的面积为Sn.查看答案和解析>>
科目:初中数学 来源:2011年海南省琼海市嘉积中学海桂学校初三数学竞赛选拔试卷(解析版) 题型:解答题
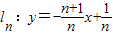 (n是正整数).当n=1时,直线l1:y=-2x+1与 x轴和y轴分别交于点A1和B1,设△A1OB1(O是平面直角坐标系的原点)的面积为s1;当n=2时,直线
(n是正整数).当n=1时,直线l1:y=-2x+1与 x轴和y轴分别交于点A1和B1,设△A1OB1(O是平面直角坐标系的原点)的面积为s1;当n=2时,直线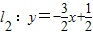 与x轴和y轴分别交于点A2和B2,设△A2OB2的面积为s2,…,依此类推,直线ln与x轴和y轴分别交于点An和Bn,设△AnOBn的面积为Sn.
与x轴和y轴分别交于点A2和B2,设△A2OB2的面积为s2,…,依此类推,直线ln与x轴和y轴分别交于点An和Bn,设△AnOBn的面积为Sn.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com