
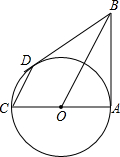
 如图,AB与⊙O相切于点A,AC为⊙O的直径,且AC=6,CD∥BO,CD交⊙O于D,连接BD.
如图,AB与⊙O相切于点A,AC为⊙O的直径,且AC=6,CD∥BO,CD交⊙O于D,连接BD.分析 (1)欲证明BD与⊙O相切,只要证明∠BDO=∠BAO=90°,可以通过证明△BOA≌△BOD即可证明.
(2)连接AD,设CD=a,BO=b,想办法列出方程组,最后在RT△AOB中利用勾股定理解决.
解答 (1)证明:连接OD.
∵AB是⊙O切线,
∴∠BAO=90°,
∵CD∥OB,
∴∠AOB=∠C,∠ODC=∠BOD,
∵OD=OC,
∴∠C=∠ODC,
∴∠BOA=∠BOD,
在△BOD和△BOA中,
$\left\{\begin{array}{l}{BO=BO}\\{∠BOA=∠BOD}\\{OA=OD}\end{array}\right.$,
∴△BOA≌△BOD,
∴∠BDO=∠BAO=90°,
∴OD⊥BD,
∴BD是⊙O的切线.
(2)连接AD,设CD=a,BO=b,
∵AC是直径,
∴∠ADC=∠BA0=90°,
∵∠AOB=∠C,
∴△OAB∽△CDA,
∴$\frac{OA}{CD}$=$\frac{OB}{AC}$,
∴$\frac{3}{a}$=$\frac{b}{6}$,
∴ab=18,又a+b=11,
∴a=2,b=9或a=9,b=2(舍弃),
∴CD=2,OB=9,
在RT△AOB中,∵∠OAB=90°,OB=9,OA=3,
∴AB=$\sqrt{O{B}^{2}-O{A}^{2}}$=$\sqrt{{9}^{2}-{3}^{2}}$=6$\sqrt{2}$.
点评 本题考查切线的判定和性质、全等三角形的判定和性质、勾股定理等知识,解题的关键是正确寻找全等三角形,学会转化的思想,把问题转化为方程组解决,属于中考常考题型.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:选择题
| 衡量指标 | 小敏 | 小芳 | 小聪 | 小明 |
| 平均数 | 90 | 85 | 90 | 85 |
| 方差 | 3 | 3 | 10 | 12 |
| A. | 小明 | B. | 小芳 | C. | 小聪 | D. | 小敏 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在?ABCD中,连接BD,BD⊥BC,CD=4,sinC=$\frac{3}{4}$,则?ABCD的面积是3$\sqrt{7}$.
如图,在?ABCD中,连接BD,BD⊥BC,CD=4,sinC=$\frac{3}{4}$,则?ABCD的面积是3$\sqrt{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
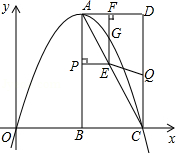 如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0),C(8,0),D(8,8),抛物线y=ax2+bx过A,C两点,动点P从点A出发,沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD向终点D运动,速度均为每秒1个单位长度,运动时间为t秒,过点P作PE⊥AB交AC于点E.
如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0),C(8,0),D(8,8),抛物线y=ax2+bx过A,C两点,动点P从点A出发,沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD向终点D运动,速度均为每秒1个单位长度,运动时间为t秒,过点P作PE⊥AB交AC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com