
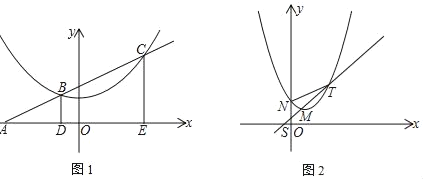
【题目】如图,已知直线:y=kx+3k与x轴交于A点,与抛物线y=![]() +1交于点B、C两点
+1交于点B、C两点
(1)若k=1,求点B、C(点B在点C的左边)的坐标;
(2)过B、C分别作x轴的垂线,垂足分别为点D、E,求ADAE的值;
(3)将抛物线y=![]() +1沿直线y=mx+1(m>1)向右平移t个单位,直线y=mx+1交y轴于S,交新抛物线于MT,N是新抛物线与y轴的交点,试探究t为何值时,NT∥x轴?
+1沿直线y=mx+1(m>1)向右平移t个单位,直线y=mx+1交y轴于S,交新抛物线于MT,N是新抛物线与y轴的交点,试探究t为何值时,NT∥x轴?
【答案】(1)点B、C的坐标分别为![]() ;(2)13;(3)t=4m
;(2)13;(3)t=4m
【解析】
(1)联立直线和抛物线表达式即可求解;
(2)设点BC的横坐标分别为x1,x2,将直线表达式与抛物线表达式联立用韦达定理求出:x1+x2=4k,x1x2=4﹣12k,ADAE=(x1+3)(x2+3)即可求解;
(3)求出N(0,![]() +mt+1);再用韦达定理,求出点T的坐标(t+4m,mt+4m2+1),NT∥x轴,则yT=yN,即可求解.
+mt+1);再用韦达定理,求出点T的坐标(t+4m,mt+4m2+1),NT∥x轴,则yT=yN,即可求解.
(1)k=1时,联立直线和抛物线表达式得: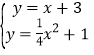 ,解得:x=2±2
,解得:x=2±2![]() ,
,
故:点B、C的坐标分别为(2﹣2![]() ,5﹣2
,5﹣2![]() )、(2+2
)、(2+2![]() ,5+2
,5+2![]() );
);
(2)设点BC的横坐标分别为x1,x2,
y=kx+3k,令y=0,则x=﹣3,即点A(﹣3,0),
将直线表达式:y=kx+3k与抛物线表达式y=![]() +1联立并整理得:
+1联立并整理得:
x2﹣4kx+(4﹣12k)=0,
则:x1+x2=4k,x1x2=4﹣12k,
ADAE=(x1+3)(x2+3)=x1x2+3(x1+x2)+9=4﹣12k+12k+9=13;
(3)设抛物线沿直线向右平移t个单位,相当于同时向上移动了mt个单位,则点M坐标为(t,1+mt),
平移后的抛物线为:y=![]() (x﹣t)2+(1+mt)…①,则点N(0,
(x﹣t)2+(1+mt)…①,则点N(0,![]() +mt+1),
+mt+1),
直线y=mx+1(m>1)…②,
将①②联立并整理得:x2﹣2xt﹣4mx+t2+4mt=0,
x1+x2=2t+4m,
由题意得:x1=xM=t,
∴x2=t+4m=xT,
则点T的坐标为(t+4m,mt+4m2+1),
NT∥x轴,则yT=yN,
即:![]() +mt+1=mt+4m2+1,
+mt+1=mt+4m2+1,
解得:t=4m.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
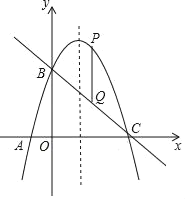
【题目】已知二次函数y=ax2+bx+3的图象经过A(﹣1,0)、C(3,0)、并且与y轴相交于点B,点P是直线BC上方的抛物线上的一动点,PQ∥y轴交直线BC于点Q.
(1)求此二次函数的表达式;
(2)求线段PQ的最大值;
(3)在抛物线的对称轴上,是否存在点M,使△MAB为等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数![]() ,当
,当![]() 时,函数有最大值
时,函数有最大值![]() .
.
(1)求此二次函数图象与坐标轴的交点;
(2)将函数![]() 图象
图象![]() 轴下方部分沿
轴下方部分沿![]() 轴向上翻折,得到的新图象,若点
轴向上翻折,得到的新图象,若点![]() 是翻折得到的抛物线弧部分上任意一点,若关于
是翻折得到的抛物线弧部分上任意一点,若关于![]() 的一元二次方程
的一元二次方程![]() 恒有实数根时,求实数
恒有实数根时,求实数![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD为△ABC外接圆⊙O的直径,且∠BAE=∠C.
(1)求证:AE与⊙O相切于点A;
(2)若AE∥BC,BC=2![]() ,AC=2
,AC=2![]() ,求AD的长.
,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
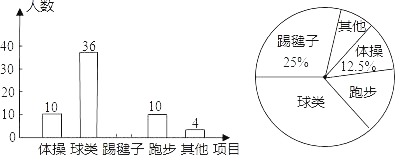
【题目】为了了解全校1800名学生对学校设置的体操、球类、跑步、踢毽子等课外体育活动项目的喜爱情况,在全校范围内随机抽取了若干名学生.对他们最喜爱的体育项目(每人只选一项)进行了问卷调查,将数据进行了统计并绘制成了如图所示的频数分布直方图和扇形统计图(均不完整).
(1)补全频数分布直方图;
(2)求扇形统计图中表示“踢毽子”项目扇形圆心角的度数.
(3)估计该校1800名学生中有多少人最喜爱球类活动?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“饺子“又名“交子”或者“娇耳”,是新旧交替之意,它是重庆人民的年夜饭必吃的一道美食.今年除夕,小侨跟着妈妈一起包饺子准备年夜饭,体验浓浓的团圆气氛.已知小侨家共10人,平均每人吃10个饺子,计划用10分钟将饺子包完.
(1)若妈妈每分钟包饺子的速度是小侨速度的2倍少2个,那么小侨每分钟至少要包多少个饺子?
(2)小侨以(1)问中的最低速度,和妈妈同时开始包饺子,妈妈包饺子的速度在(1)问的最低速度基础上提升了![]() a%,在包饺子的过程中小侨外出耽误了
a%,在包饺子的过程中小侨外出耽误了![]() 分钟,返家后,小侨与妈妈一起包完剩下的饺子,所用时间比原计划少了
分钟,返家后,小侨与妈妈一起包完剩下的饺子,所用时间比原计划少了![]() a%,求a的值.
a%,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=![]() x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.

(1)求抛物线的解析式;(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 中,
中,![]() ,
,![]() 是
是![]() 的中点.将
的中点.将![]() 沿
沿![]() 对折至
对折至![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,则下列结论正确的有( )个.
,则下列结论正确的有( )个.
(1)![]() (2)
(2)![]()
(3)![]() 的面积是18 (4)
的面积是18 (4)![]()

A. 4B. 3C. 2D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发沿
出发沿![]() 向点
向点![]() 匀速运动,速度为
匀速运动,速度为![]() ,同时,点
,同时,点![]() 从点
从点![]() 出发沿
出发沿![]() 向点
向点![]() 匀速运动,速度为
匀速运动,速度为![]() ,当点
,当点![]() 停止运动时,点
停止运动时,点![]() 也随之停止运动,过点
也随之停止运动,过点![]() 做
做![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() .设运动的时间为
.设运动的时间为![]() .
.
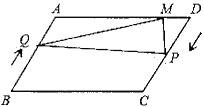
(1)当![]() 时,求
时,求![]() 的值;
的值;
(2)是否存在某一时刻![]() ,使得
,使得![]() 的面积是平行四边形
的面积是平行四边形![]() 面积的
面积的![]() ?若存在,求出相应
?若存在,求出相应![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(3)过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,是否存在某一时刻
,是否存在某一时刻![]() ,使得
,使得![]() 在线段
在线段![]() 的垂直平分线上?若存在,求出相应
的垂直平分线上?若存在,求出相应![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com