
 如图,四边形OABC为直角梯形,已知AB∥OC,BC⊥OC,A点坐标为(3,4),AB=6.
如图,四边形OABC为直角梯形,已知AB∥OC,BC⊥OC,A点坐标为(3,4),AB=6.分析 (1)设OA的解析式为y=kx,依题意可得k值.
(2)延长BA交y轴于点D.推出AD=3,OD=4.根据勾股定理推出AO的值.然后推出OC,BC的长.可求梯形周长.
(3)根据题意直线l把梯形方程两个梯形,设出直线l和上底的交点坐标,由总面积为30,用梯形OAED的面积等于15,就出交点坐标,即可;
(4)根据2可得被l分成的两部分分别为10和14,故要分两种情况讨论.求出点P的坐标,设PD的解析式为y=mx+n,利用待定系数法求出直线PD的解析式
解答 解:(1)设OA的解析式为y=kx,
则3k=4,
∴k=$\frac{4}{3}$.
∴OA的解析式为y=$\frac{4}{3}$x.
(2)如图,延长BA交y轴于点D.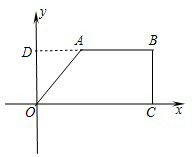
∵BA∥OC,
∴AD⊥y轴.且AD=3,OD=4.
∴AO=5,∴DB=3+6=9.
∴OC=9,又BC=OD=4.
∴COABC=OA+AB+BC+OC=5+6+4+9=24.
(3)如图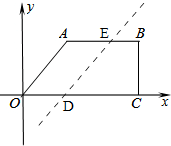
设点E的坐标为(a,4),
∴AE=a-3,
由(2)得AB=6,OC=9,BC=4,
∴S梯形OABC=$\frac{1}{2}$(AB+OC)×BC=$\frac{1}{2}$(6+9)×4=30,
∵直线l经过点D(3,0),
∴OD=3,
∵直线l将直角梯形OABC的面积分成相等的两部分,
∴S梯形OAED=$\frac{1}{2}$S梯形OABC=$\frac{1}{2}$×30=15,
∴S梯形OAED=$\frac{1}{2}$(AE+OD)×BC=$\frac{1}{2}$×(a-3+3)×4=15,
∴a=$\frac{9}{2}$,
∴E($\frac{9}{2}$,4),
∵D(3,0),
∴直线解析式为y=$\frac{8}{3}$x-8.
(4)∵COABC=24,故被l分成的两部分分别为10和14.
若l左边部分为10,则s=10-3=7,
∴P(5,4).
设PD为:y=mx+n,则$\left\{\begin{array}{l}{5m+n=4}\\{3m+n=0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{m=2}\\{n=-6}\end{array}\right.$,
∴y=2x-6;
若l左边部分为14,则s=14-3=11,
∴P(9,4).
∴$\left\{\begin{array}{l}{9m+n=4}\\{3m+n=0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{m=\frac{2}{3}}\\{n=-2}\end{array}\right.$,
∴y=$\frac{2}{3}$x-2.
点评 此题是一次函数综合题,主要考查了待定系数法,梯形的面积,周长,解本题的关键是求出梯形OABC的周长和面积.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解CCTV1传统文化类节目《中国诗词大会》的收视率 | |
| B. | 了解初一(1)班学生的身高情况 | |
| C. | 了解庞各庄某地块出产西瓜的含糖量 | |
| D. | 调查某品牌笔芯的使用寿命 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com