
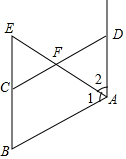
 如图,AD∥BE,AE平分∠BAD,CD与AE相交于F,∠CFE=∠E.则AB与CD有何位置关系?试说明理由.
如图,AD∥BE,AE平分∠BAD,CD与AE相交于F,∠CFE=∠E.则AB与CD有何位置关系?试说明理由. 科目:初中数学 来源: 题型:解答题
 已知直线y=-2x+2分别与x轴,y轴交于点C,B,并且与某一反比例函数y=$\frac{m}{x}$在第二象限交于点A(-1,a),过点B作直线AC的垂线交x轴于点E,交另一双曲线y=$\frac{n}{x}$于点D(b,-2).
已知直线y=-2x+2分别与x轴,y轴交于点C,B,并且与某一反比例函数y=$\frac{m}{x}$在第二象限交于点A(-1,a),过点B作直线AC的垂线交x轴于点E,交另一双曲线y=$\frac{n}{x}$于点D(b,-2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 某小组在“用频率估计概率”的实验中,统计了某种结果出现的频率,绘制了如图所示的折线图,那么符合这一结果的实验最有可能的是( )
某小组在“用频率估计概率”的实验中,统计了某种结果出现的频率,绘制了如图所示的折线图,那么符合这一结果的实验最有可能的是( )| A. | 袋子中有1个红球和2个黄球,它们只有颜色上的区别,从中随机地取出一个球是黄球 | |
| B. | 掷一个质地均匀的正六面体骰子,落地时面朝上的点数是6 | |
| C. | 在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀” | |
| D. | 掷一枚质地均匀的硬币,落地时结果是“正面向上” |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
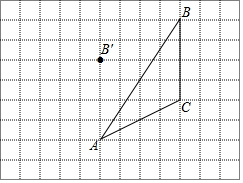 如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.
如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.
如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com