
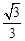 x+1�ֱ����������ύ��B��A���㣬CΪ��ֱ���ϵ�һ���㣬��ÿ��1����λ���ȵ��ٶȴӵ�A��ʼ��ֱ��BA�����ƶ������ȱߡ�CDE����D�͵�E����x���ϣ��Ե�CΪ�����������y=a��x��m��2+n������E����M��x�ᡢֱ��AB�����У���뾶Ϊ3��1��
x+1�ֱ����������ύ��B��A���㣬CΪ��ֱ���ϵ�һ���㣬��ÿ��1����λ���ȵ��ٶȴӵ�A��ʼ��ֱ��BA�����ƶ������ȱߡ�CDE����D�͵�E����x���ϣ��Ե�CΪ�����������y=a��x��m��2+n������E����M��x�ᡢֱ��AB�����У���뾶Ϊ3��1�� ��a��
��a��
 ��
�� ��
��
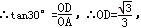
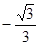 ��0����E�������ǣ�
��0����E�������ǣ�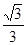 ��0����
��0����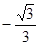 ��0����E��
��0����E��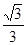 ��0�������� y=a��x-m��2+n��
��0�������� y=a��x-m��2+n��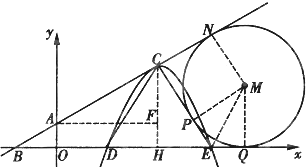
 ��a��a��0����
��a��a��0����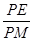 ����PE=��
����PE=�� -3��a
-3��a ��a+��
��a+�� -3��a=-2
-3��a=-2 a
a a��CH=-3a��BH=-3
a��CH=-3a��BH=-3 a��
a�� a-
a- ��OE=-4
��OE=-4 a-
a-
 a-
a- ��0��
��0�� a-
a- ��-3a��
��-3a�� a+
a+ ��2-3a
��2-3a a-
a- +3
+3 a+
a+ ��2-3a=0
��2-3a=0 ��CF=2����AC=4
��CF=2����AC=4


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ ���ͣ������
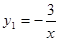 ��x��0����ͼ���ཻ��A�㣬��y�ᡢx��ֱ��ཻ��B��C���㣬��C��2��0����A��ĺ�����Ϊ-1.
��x��0����ͼ���ཻ��A�㣬��y�ᡢx��ֱ��ཻ��B��C���㣬��C��2��0����A��ĺ�����Ϊ-1.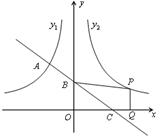
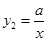 ��x��0����ͼ����
��x��0����ͼ����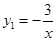 ��x��0����ͼ�����y��Գƣ���
��x��0����ͼ�����y��Գƣ���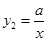 ��x��0����ͼ����ȡһ��P��P��ĺ��������2������P����PQ��x�ᣬ������Q�����ı���BCQP���������2����P������꣮
��x��0����ͼ����ȡһ��P��P��ĺ��������2������P����PQ��x�ᣬ������Q�����ı���BCQP���������2����P������꣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
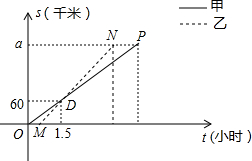
 �ֱ��ʾ�ڹ���������е�·�̣�tΪʱ�䣬������ͼ������������Ǻϵ��ǣ� ��
�ֱ��ʾ�ڹ���������е�·�̣�tΪʱ�䣬������ͼ������������Ǻϵ��ǣ� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
 �뺯��
�뺯�� ��ͬһ����ϵ�еĴ���ͼ������ͼ�е� �� ��
��ͬһ����ϵ�еĴ���ͼ������ͼ�е� �� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
| A��y=0.5t��8<t��12�� | B��y=0.5t+2��8<t��12�� |
| C��y=0.5t+8��8<t��12�� | D��y="0." 5t-2��8<t��12�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
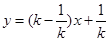 ������ʵ��k����0��k��1��
������ʵ��k����0��k��1��| A��1 | B��2������ | C��k������ | D��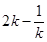 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
| ��� | �ʵ� | ���� | ϴ�»� |
| ���� | 2000 | 1600 | 1000 |
| �ۼ� | 2200 | 1800 | 1100 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com