
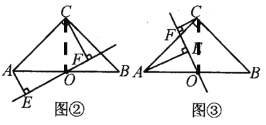
【题目】如图,在△ABC中,∠ACB=90,∠ABC=45 ,点O是AB的中点,过A、C两点向经过点O的直线作垂线,垂足分别为E、F.
(1)如图①,求证:EF=AE+CF.
(2)如图②,图③,线段EF、AE、CF之间又有怎样的数量关系?请直接写出你的猜想.

【答案】(1)见解析;(2)图②:EF=AE+CF 图③:EF=AE-CF,见解析
【解析】
(1)连接OC,运用AAS证△AOE≌△OCF即可;
(2)按(1)中的方法,连接OC,证明△AOE≌△OCF,即可得出结论
(1)连接OC,∵△ABC是等腰直角三角形,
∴∠AOC=90°,AO=CO,
∵∠AOE+∠COF=90°,∠EAO+∠AOE=90°,
∴∠EAO=∠COF,
又∵AO=CO,∠AEO=∠CFO,
∴△AOE≌△OCF(AAS)
∴OE=CF,AE=OF ∴EF=AE+CF

(2)如图②,连接OC,
∵△ABC是等腰直角三角形,
∴∠AOC=90°,AO=CO,
∵∠AOE+∠COF=90°,∠EAO+∠AOE=90°,
∴∠EAO=∠COF,
又∵AO=CO,∠AEO=∠CFO,
∴△AOE≌△OCF(AAS)
∴OE=CF,AE=OF
∴EF=AE+CF.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:初中数学 来源: 题型:
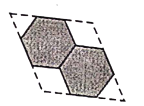
【题目】校园内有一个由两个全等的六边形(边长为![]() )围成的花坛,现将这个花坛在原有的基础上扩建成如图所示的一个菱形区域,并在新扩建的部分种上草坪,则扩建后菱形区域的周长为( )
)围成的花坛,现将这个花坛在原有的基础上扩建成如图所示的一个菱形区域,并在新扩建的部分种上草坪,则扩建后菱形区域的周长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
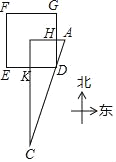
【题目】《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步面见木?”用今天的话说,大意是:如图,DEFG是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门H位于GD的中点,南门K位于ED的中点,出东门15步的A处有一树木,求出南门多少步恰好看到位于A处的树木(即点D在直线AC上)?请你计算KC的长为多少步.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线 y = x与反比例函数![]() 的图象交于点A(2,m).
的图象交于点A(2,m).

(1)求m和k的值;
(2)点P(xP,yP)是函数![]() 图象上的任意一点,过点P作平行于x轴的直线,交直线y=x于点B.
图象上的任意一点,过点P作平行于x轴的直线,交直线y=x于点B.
①当yP = 4时,求线段BP的长;
②当BP![]() 3时,结合函数图象,直接写出点P 的纵坐标yP的取值范围.
3时,结合函数图象,直接写出点P 的纵坐标yP的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②b<a+c;③4a+2b+c>0;④2c–3b<0;⑤a+b>n(an+b)(n≠1),其中正确的结论有( )
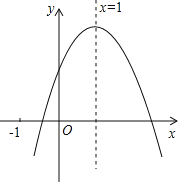
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:函数y=﹣x2+mx+2m(m为常数)的图象不经过第二象限,当﹣5≤x≤1时,函数的最大值与最小值之差为12.25,则m的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平面直角坐标系xOy中,直线y=![]() x+
x+![]() 与x轴交于点A,与y轴交于点B,点F是点B关于x轴的对称点,抛物线y=
与x轴交于点A,与y轴交于点B,点F是点B关于x轴的对称点,抛物线y=![]() x2+bx+c经过点A和点F,与直线AB交于点C.
x2+bx+c经过点A和点F,与直线AB交于点C.
(1)求b和c的值;
(2)点P是直线AC下方的抛物线上的一动点,连结PA,PB.求△PAB的最大面积及点P到直线AC的最大距离;
(3)点Q是抛物线上一点,点D在坐标轴上,在(2)的条件下,是否存在以A,P,D,Q为顶点且AP为边的平行四边形,若存在,直接写出点Q的坐标;若不存在,说明理由.
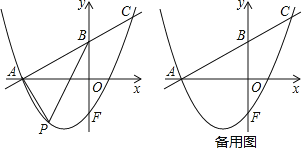
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD的边AB上任取一点E,作EF⊥AB交BD于点F,取FD的中点G,连接EG、CG,如图(1),易证 EG=CG且EG⊥CG.

(1)将△BEF绕点B逆时针旋转90°,如图(2),则线段EG和CG有怎样的数量关系和位置关系?请直接写出你的猜想.
(2)将△BEF绕点B逆时针旋转180°,如图(3),则线段EG和CG又有怎样的数量关系和位置关系?请写出你的猜想,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,平行四边形ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
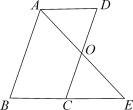
(1)求证:△AOD≌△EOC;
(2)连接AC、DE,当∠B=∠AEB=45°时,求证四边形 ACED是正方形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com