
| | ���ۣ�Ԫ/̨�� | �ۼۣ�Ԫ/̨�� |
| ���� |  | 2500 |
| �ʵ� |  | 2000 |
 ��
�� �����a=2000��
�����a=2000�� ����ã�
����ã� ��
�� ��xȡ������
��xȡ������

 С��ſ�ʱ��ҵϵ�д�
С��ſ�ʱ��ҵϵ�д� һ������ϵ�д�
һ������ϵ�д� �Ƹ�С״Ԫ���ֳ������ϵ�д�
�Ƹ�С״Ԫ���ֳ������ϵ�д� �¸��̵�ѧϵ�д�
�¸��̵�ѧϵ�д� ����ͬѧһ����ʦȫ�źþ�ϵ�д�
����ͬѧһ����ʦȫ�źþ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
 �У�
�У� ��ֵ��
��ֵ�� ���������С����
���������С���� ��ȡֵ��Χ�ǣ��� ����
��ȡֵ��Χ�ǣ��� ����A�� | B�� | C�� | D�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��

| A��x="2" | B��y="2" | C��x="-1" | D��y="-1" |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
 ��
�� �Ḻ���ᡢ
�Ḻ���ᡢ ��������ֱ���A��B���㣬����������
��������ֱ���A��B���㣬���������� ��ͼ����ֱ��AB���ڵ�Q����A��B����ֱ���AM��OQ��M��BN��OQ��N����AM =10��BN =3��
��ͼ����ֱ��AB���ڵ�Q����A��B����ֱ���AM��OQ��M��BN��OQ��N����AM =10��BN =3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
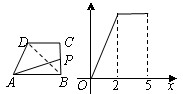
 ��AB��CD��
��AB��CD�� ��
�� ����
���� �ӵ�
�ӵ� ��������
�������� ��
�� �˶�����
�˶����� ֹͣ�����
ֹͣ����� �˶���·��Ϊ
�˶���·��Ϊ ��
�� �����Ϊ
�����Ϊ �����
����� ����
���� �ĺ���ͼ����ͼ��ʾ����
�ĺ���ͼ����ͼ��ʾ���� ������ǣ� ��
������ǣ� ��| A��3 | B��4 | C��5 | D��6 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com