
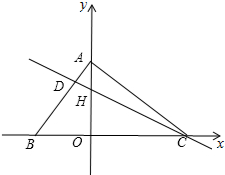
 ��ͼ����ƽ��ֱ������ϵxOy�У���ABC�Ķ���A��y���ϣ�BC����x���غϣ���C����AB�Ĵ��߷ֱ�AB��y���ڵ�D��H��AB=HC���߶�OB��OC��OB��OC���ij��Ƿ���x2-6x+8=0�ĸ���
��ͼ����ƽ��ֱ������ϵxOy�У���ABC�Ķ���A��y���ϣ�BC����x���غϣ���C����AB�Ĵ��߷ֱ�AB��y���ڵ�D��H��AB=HC���߶�OB��OC��OB��OC���ij��Ƿ���x2-6x+8=0�ĸ������� ��1��֤����AOB�ա�COH�������OH=OB������õ�H���꣬���ô���ϵ���������ֱ��CD�Ľ���ʽ��
��2���ֵ�P��ԭ�������Ҳ࣬�ֱ���t��ʾ��OP��OQ�ij��������S��t�ĺ�����ϵʽ��
��3���������ɵ�OP=OQ���ɣ�2���ɵõ�����t�ķ��̣������t��ֵ�������M������꣮
��� �⣺��1����CD��AB��
���BAO+��ABO=��OCH+��ABO=90�㣬
���BAO=��OCH��
�ڡ�AOB�͡�COH�У�
$\left\{\begin{array}{l}{��BAO=��OCH}\\{��AOB=��HCO}\\{AB=CH}\end{array}\right.$��
���AOB�ա�COH��AAS����
��OB=OH��
�ⷽ��x2-6x+8=0�ɵ�x=2��x=4��
��OB=2��OC=4��
��OH=2��
��C��4��0����H��0��2����
��ֱ��CD����ʽΪy=kx+b��
��C��H������������ɵ�$\left\{\begin{array}{l}{4k+b=0}\\{b=2}\end{array}\right.$��
���$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=2}\end{array}\right.$��
��ֱ��CD����ʽΪy=-$\frac{1}{2}$x+2��
��2������P��ԭ����࣬��0��t��2ʱ������PQ����ͼ1��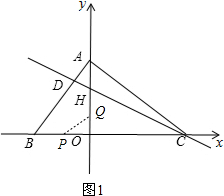
��OP=OB-BP=2-t��
��2BP=3OQ��
��OQ=$\frac{2}{3}$BP=$\frac{2}{3}$t��
��S=$\frac{1}{2}$OP•OQ=$\frac{1}{2}$•$\frac{2}{3}$t��2-t��=-$\frac{1}{3}$t2+$\frac{2}{3}$t��
��P��ԭ���Ҳ࣬��2��t��6ʱ������PQ����ͼ2��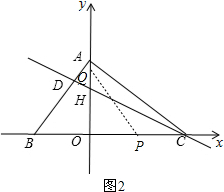
��OP=BP-OB=t-2��
��2BP=3OQ��
��OQ=$\frac{2}{3}$BP=$\frac{2}{3}$t��
��S=$\frac{1}{2}$OP•OQ=$\frac{1}{2}$•$\frac{2}{3}$t��t-2��=$\frac{1}{3}$t2-$\frac{2}{3}$t��
���Ͽ�֪S��t�Ĺ�ϵʽΪS=$\left\{\begin{array}{l}{-\frac{1}{3}{t}^{2}+\frac{2}{3}t��0��t��2��}\\{\frac{1}{3}{t}^{2}-\frac{2}{3}t��2��t��6��}\end{array}\right.$��
��3����P����ԭ�����ʱ����ͼ3��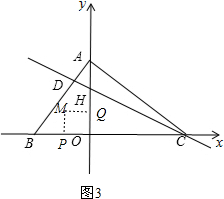
�ɣ�2����֪OP=2-t��OQ=$\frac{2}{3}$t��
���ı���OPMQΪ�����Σ�
��OP=OQ��
��2-t=$\frac{2}{3}$t�����t=$\frac{6}{5}$��
��OP=OM=2-t=$\frac{4}{5}$��
��M��-$\frac{4}{5}$��$\frac{4}{5}$����
��P����ԭ���Ҳ�ʱ����ͼ4��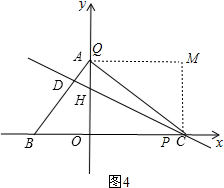
�ɣ�2����֪OP=t-2��OQ=$\frac{2}{3}$t��
���ı���OPMQΪ�����Σ�
��OP=OQ��
��t-2=$\frac{2}{3}$t�����t=6��
��OP=OM=t-2=4��
��M��4��4����
���Ͽ�֪�������������ĵ�M����M������Ϊ��-$\frac{4}{5}$��$\frac{4}{5}$����4��4����
���� ������Ҫ����һ�κ������ۺ�Ӧ�ã��漰����ϵ������ȫ�������ε��ж������ʡ������ε����ʡ�������ϵʽ��֪ʶ�㣮�ڣ�1����֤��������ȫ�����H�������ǽ���Ĺؼ����ڣ�2������t�ֱ��ʾ��OP��OQ�ǽ���Ĺؼ���ע�����˼���Ӧ�ã��ڣ�3�������������ε��ı�������t�ǽ���Ĺؼ��������漰֪ʶ��϶࣬�ۺ��Խ�ǿ���Ѷ����У�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
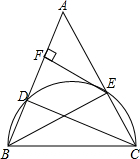 �ڵ�����ABC�У�AB=AC����BCΪֱ������Բ��AB��AC��D��E����E�����߽�AB��F����EF��AB�����A��
�ڵ�����ABC�У�AB=AC����BCΪֱ������Բ��AB��AC��D��E����E�����߽�AB��F����EF��AB�����A���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com