
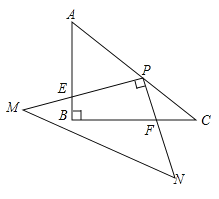
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=8,Rt△MPN,∠MPN=90°,点P在AC上,PM交AB与点E,PN交BC与点F,当PE=2PF时,AP=_____
【答案】6
【解析】
如图作PQ⊥AB于Q,PR⊥BC于R.由△QPE∽△RPF,推出![]() ,可得PQ=2PR=2BQ,由PQ∥BC,可得AQ∶QP∶AP=AB∶BC∶AC=6∶8∶10=3∶4∶5,设PQ=4x,则AQ=3x,AP=5x,BQ=2x,可得2x+3x=6,求出x即可解决问题.
,可得PQ=2PR=2BQ,由PQ∥BC,可得AQ∶QP∶AP=AB∶BC∶AC=6∶8∶10=3∶4∶5,设PQ=4x,则AQ=3x,AP=5x,BQ=2x,可得2x+3x=6,求出x即可解决问题.
解:如图,作PQ⊥AB于Q,PR⊥BC于R.
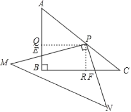
∵∠PQB=∠QBR=∠BRP=90°,
∴四边形PQBR是矩形,
∴∠QPR=90°=∠MPN,
∴∠QPE=∠RPF,
∴△QPE∽△RPF,
∴![]() ,
,
∴PQ=2PR=2BQ,
∵PQ∥BC,
∴AQ∶QP∶AP=AB∶BC∶AC=6∶8∶10=3∶4∶5,
设PQ=4x,则AQ=3x,AP=5x,BQ=2x,
∴2x+3x=6,
∴x=![]() ,
,
∴AP=5x=6.
故答案为6.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要求写自变量的取值范围)
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
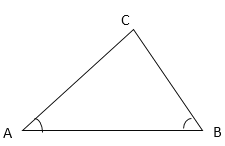
【题目】为维护我国海洋权益,强化管辖海域的实际控制,国家海洋局决定实施常态化的海洋维权巡航执法,开展多种形式的海洋维权行动:外国船只除特许外,不得进入我国海洋100海里以内的区域.如图,设A、B是我们的观察站,A和B之间的距离为160海里,海岸线是过A、B的一条直线.一外国船只在C点,在A点测得∠BAC=45°,同时在B点测得∠ABC=60°,问此时是否要向外国船只发出警告,令其退出我国海域.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O是边长为6的等边△ABC的外接圆,点D,E分别是BC,AC上两点,且BD=CE,连接AD,BE相交于点P,延长线段BE交⊙O于点F,连接CF.


(1)求证:AD∥FC;
(2)连接PC,当△PEC为直角三角形时,求tan∠ACF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,∠A=90°.
(1)请用圆规和直尺作出⊙P,使圆心P在AC边上,且与AB,BC两边都相切(保留作图痕迹,不写作法和证明);

(2)在(1)的条件下,若∠B=45°,AB=1,⊙P切BC于点D,求劣弧![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D、E是以AB为直径的圆O上两点,且∠AED=45°,过点D作DC∥AB.
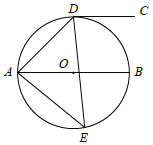
(1)请判断直线CD与圆O的位置关系,并说明理由;
(2)若圆O的半径为![]() ,
,![]() ,求AE的长;
,求AE的长;
(3)过点D作![]() ,垂足为F,直接写出线段AE、BE、DF之间的数量关系 .
,垂足为F,直接写出线段AE、BE、DF之间的数量关系 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠ADE、∠CDF分别交BC、AB于点E、F,DF交对角线AC于点M,且∠ADE=∠CDF.
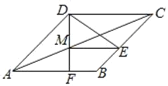
(1)求证:CE=AF;
(2)连接ME,若![]() =
=![]() ,AF=2,求
,AF=2,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,AC为直径,点D为弧ACB的中点,过点D的切线与BC的延长线交于点E.
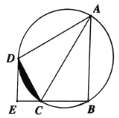
(1)用尺规作图作出圆心O;(保留作图痕迹,不写作法);
(2)求证:DE⊥BC;
(3)若OC=2CE=4,求图中阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如下的表格,则符合这一结果的实验最有可能的是( )
实验次数 | 100 | 200 | 300 | 500 | 800 | 1000 | 2000 |
频率 | 0.365 | 0.328 | 0.330 | 0.334 | 0.336 | 0.332 | 0.333 |
A.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
B.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
C.抛一个质地均匀的正六面体骰子,向上的面点数是5
D.抛一枚硬币,出现反面的概率
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com