练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，在□ABCD中，E、F分别是AB、CD的中点，连接AF、CE．

    （1）求证：△BEC≌△DFA；

    （2）连接AC，当CA＝CB时，判断四边形AECF是什么特殊四边形？并证明你的结论．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：]辽宁省兴城市2016-2017学年七年级下学期期中考试数学试卷 题型：解答题

    如图（1），在平面直角坐标系中，A（a，0），C（b，2），过C作CB⊥x轴，且满足（a+b）2+=0．

    （1）求三角形ABC的面积．

    （2）若过B作BD∥AC交y轴于D，且AE，DE分别平分∠CAB，∠ODB，如图2，求∠AED的度数．

    （3）在y轴上是否存在点P，使得三角形ABC和三角形ACP的面积相等？若存在，求出P点坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：广东省广州市黄埔区2014-2015学年中考数学一模试卷 题型：选择题

    如果点E，F，G，H分别是菱形ABCD四边AB，BC，CD，DA上的中点，那么四边形EFGH是（ ）．

    （A）菱形 （B）矩形 （C）正方形 （D）以上都不是

    查看答案和解析>>

    科目：初中数学 来源：2018年春八年级数学下册（沪科版）：第十九章 整合提升密码 题型：解答题

    已知E，F分别为正方形ABCD的边BC，CD上的点，AF，DE相交于点G，当E，F分别为边BC，CD的中点时，有：①AF=DE；②AF⊥DE成立．

    试探究下列问题：

    （1）如图1，若点E不是边BC的中点，F不是边CD的中点，且CE=DF，上述结论①，②是否仍然成立？（请直接回答“成立”或“不成立”），不需要证明）

    （2）如图2，若点E，F分别在CB的延长线和DC的延长线上，且CE=DF，此时，上述结论①，②是否仍然成立？若成立，请写出证明过程，若不成立，请说明理由；

    （3）如图3，在（2）的基础上，连接AE和EF，若点M，N，P，Q分别为AE，EF，FD，AD的中点，请判断四边形MNPQ是“矩形、菱形、正方形”中的哪一种，并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源：2018年春八年级数学下册（沪科版）：第十九章 整合提升密码 题型：单选题

    如果一个多边形的内角和等于360度，那么这个多边形的边数为（ ）

    A. 4 B. 5 C. 6 D. 7

    查看答案和解析>>

    科目：初中数学 来源：2018年春八年级数学下册（沪科版）：第十九章 整合提升密码 题型：填空题

    如图，正方形ABCD的边长为4，∠DAC的平分线交DC于点E，若点P，Q分别是AD和AE上的动点，则DQ＋PQ的最小值是________．

    查看答案和解析>>

    科目：初中数学 来源：2018年春八年级数学下册（沪科版）：第十九章 整合提升密码 题型：解答题

    已知，在矩形ABCD中，AB＝4 cm，BC＝8 cm，AC的垂直平分线EF分别交AD，BC于点E，F，垂足为O.

    (1)如图①，连接AF，CE，试说明四边形AFCE为菱形，并求AF的长；

    (2)如图②，动点P，Q分别从A，C两点同时出发，沿△AFB和△CDE各边匀速运动一周．即点P自A→F→B→A停止，点Q自C→D→E→C停止．在运动过程中，已知点P的速度为5 cm/s，点Q的速度为4 cm/s，运动时间为t s，当以A，C，P，Q四点为顶点的四边形是平行四边形时，求t的值．

    查看答案和解析>>

    科目：初中数学 来源：2018年春八年级数学下册（沪科版）：第19章达标检测卷 题型：填空题

    正方形ABCD的边长是4，点P是AD边的中点，点E是正方形边上的一点，若△PBE是等腰三角形，则腰长为________．

    查看答案和解析>>

    科目：初中数学 来源：湖北省潜江市2018届九年级10月联考数学试卷 题型：选择题

    如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=﹣1，给出四个结论：①c＞0；②若点B(-1.5,y1)、C(-2.5,y2)为函数图象上的两点，则y1＜y2；③2a﹣b=0；④ 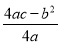＜0.其中正确结论的个数是（ ）

    A. 1 B. 2 C. 3 D. 4

    查看答案和解析>>

    同步练习册答案