
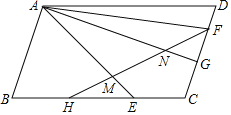
【题目】如图,在平行四边形ABCD中,点H,E在BC边上,点G,F在CD边上,连接AF,AG,AE,HF,AG垂直平分CF,HF分别交AE,AG于点M,N,∠AEB=45°,∠FHC=∠GAE.
(1)若AF=![]() ,tan∠FAG=
,tan∠FAG=![]() ,求AN;
,求AN;
(2)若∠FHC=2∠FAG,求证:![]() AE=MN+BE.
AE=MN+BE.
【答案】(1)AN=3![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)首先证明△FNG是等腰直角三角形,设FG=x,则AG=4k,利用勾股定理求出x即可解决问题.
(2)连接AH,AC.作AK⊥AE交CB速度延长线于K.设AC交FH于O.利用全等三角形的性质证明NM=BK即可解决问题.
(1)解:∵∠MHE=∠MAN,∠EMH=∠AMN,
∴∠ANM=∠MEH=45°,
∴∠FNG=∠ANM=45°,
∵AG⊥CF,
∴∠AGF=90°,
∴∠GNF=∠GFN=45°,
∴GN=GF,设GN=GF=x,
∵tan∠FAG=![]() ,
,
∴AG=4x,
∵AF2=AG2+FG2,
∴34=(4x)2+x2,
∴x=![]() 或﹣
或﹣![]() (舍弃),
(舍弃),
∴AN=3x=3![]() .
.
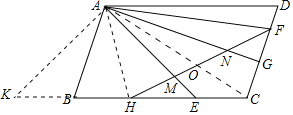
(2)证明:连接AH,AC.作AK⊥AE交CB速度延长线于K.设AC交FH于O.
∵∠KAE=90°,∠AEK=45°,
∴∠K=∠AEK=45°,
∵AG垂直平分线段CF,
∴AC=AF,
∴∠GAC=∠GAF,∠ACF=∠AFC,
∵∠FHC=2∠FAG,∠FAC=2∠FAG,
∴∠FHC=∠FAC,
∴A,H,C,F四点共圆,
∴∠AHK=∠AFC,∠AHN=∠ACF,
∴∠AHK=∠AHN,
∵∠K=∠ANH=45°,AH=AH,
∴△AHK≌△AHN(AAS),
∴AK=AN,
∵AB∥CD,AG⊥CD,
∴AG⊥AB,
∴∠GAB=∠KAE=90°,
∴∠KAB=∠NAM,
∴△KAB≌△NAM(ASA),
∴BK=MN,
∴BE+MN=BE+BK=EK=![]() AE,
AE,
即![]() AE=BE+MN.
AE=BE+MN.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
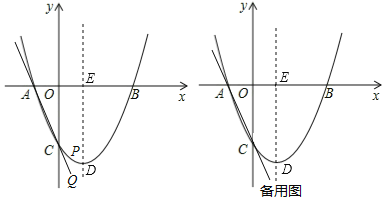
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx﹣3交x轴于点A(﹣1,0)和点B(3,0),与y轴交于点C,顶点是D,对称轴交x轴于点E.
(1)求抛物线的解析式;
(2)点P是抛物线在第四象限内的一点,过点P作PQ∥y轴,交直线AC于点Q,设点P的横坐标是m.
①求线段PQ的长度n关于m的函数关系式;
②连接AP,CP,求当△ACP面积为![]() 时点P的坐标;
时点P的坐标;
(3)若点N是抛物线对称轴上一点,则抛物线上是否存在点M,使得以点B,C,M,N为顶点的四边形是平行四边形?若存在,请直接写出线段BN的长度;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新能源汽车环保节能,越来越受到消费者的喜爱.各种品牌相继投放市场.一汽贸公司经销某品牌新能源汽车.去年销售总额为5000万元,今年1~5月份,每辆车的销售价格比去年降低1万元.销售数量与去年一整年的相同.销售总额比去年一整年的少20%,今年1~5月份每辆车的销售价格是多少万元?设今年1~5月份每辆车的销售价格为x万元.根据题意,列方程正确的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,四边形![]() 是矩形,点
是矩形,点![]() ,点
,点![]() ,点
,点![]() .以
.以![]() 点为中心,顺时针旋转矩形
点为中心,顺时针旋转矩形![]() ,得到矩形
,得到矩形![]() ,点
,点![]() 的对应点分别为
的对应点分别为![]() ,记旋转角为
,记旋转角为![]() .
.
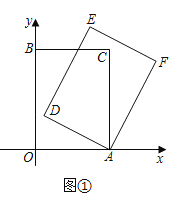
(1)如图①,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
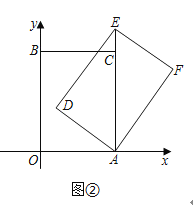
(2)如图②,当点![]() 落在
落在![]() 的延长线上时,求点
的延长线上时,求点![]() 的坐标;
的坐标;
(3)当点![]() 落在线段
落在线段![]() 上时,求点
上时,求点![]() 的坐标(直接写出结果即可).
的坐标(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ABC=90°,BD为∠ABC的角平分线,F为AC的中点,AE∥BC交BD的延长线于点E,其中∠FBC=2∠FBD.
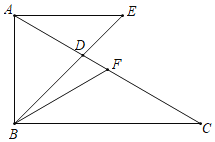
(1)求∠EDC的度数.
(2)求证:BF=AE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】袋中装有2个红球和2个绿球.
(1)先从袋中摸出1个球后放回,混合均匀后再摸出1个球,求两次摸到的球中有1个绿球和1个红球的概率;
(2)先从袋中摸出1个球后不放回,再摸出个球,则两次摸到的球中有1个绿球和1个红球的概率是 .(直接填答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c的图象如图所示,对称轴为直线x=1.以下结论:①2a>-b;②4a+2b+c>0;③m(am+b)>a+b(m是大于1的实数);④3a+c<0其中正确结论的个数为( )
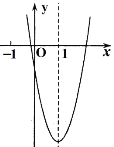
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,点
中,点![]() 为原点,点
为原点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,抛物线
,抛物线![]() 经过点
经过点![]() 、
、![]() ,与
,与![]() 交于点
交于点![]() .
.
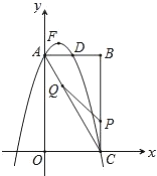
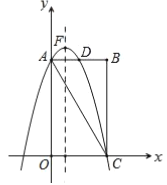
备用图
⑴求抛物线的函数解析式;
⑵点![]() 为线段
为线段![]() 上一个动点(不与点
上一个动点(不与点![]() 重合),点
重合),点![]() 为线段
为线段![]() 上一个动点,
上一个动点,![]() ,连接
,连接![]() ,设
,设![]() ,
,![]() 的面积为
的面积为![]() .求
.求![]() 关于
关于![]() 的函数表达式;
的函数表达式;
⑶抛物线![]() 的顶点为
的顶点为![]() ,对称轴为直线
,对称轴为直线![]() ,当
,当![]() 最大时,在直线
最大时,在直线![]() 上,是否存在点
上,是否存在点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,若存在,请写出符合条件的点
为顶点的四边形是平行四边形,若存在,请写出符合条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com