
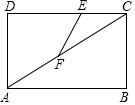
 如图,在矩形ABCD中,AB=8,AD=6,动点E从点C出发,以每秒1个单位长度的速度沿CD方向匀速运动,与此同时,动点F从点A出发,以每秒2个单位长度的速度沿对角线AC方向匀速运动,当点F到达点C时,E,F两点同时停止运动,连结EF,设运动时间为t秒.
如图,在矩形ABCD中,AB=8,AD=6,动点E从点C出发,以每秒1个单位长度的速度沿CD方向匀速运动,与此同时,动点F从点A出发,以每秒2个单位长度的速度沿对角线AC方向匀速运动,当点F到达点C时,E,F两点同时停止运动,连结EF,设运动时间为t秒.分析 (1)根据速度×时间=路程得:CE=t,AF=2t,分两种情况:
①当∠CEF=90°时,如图1,△CEF∽△CDA,②当∠EFC=90°时,如图2,△CEF∽△CAD;分别列比例式得方程解出即可;
(2)先求出E′落在两边AB和BC上时的时间t的值,再写出E′′落在△ABC的内部(不包括边上)时t的取值范围.
当点E关于点F的对称点E′落在BC上时,如图3,作辅助线构建全等三角形和相似三角形,表示出CG和GE′的长,通过相似列比例式得方程解出即可;
当点E关于点F的对称点E′落在AB上时,如图4,同理得:△EFC≌△E′FA,根据全等三角形对应边相等得等式解出即可.
解答 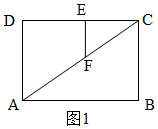 解:(1)由题意得:CE=t,AF=2t,
解:(1)由题意得:CE=t,AF=2t,
当以C,E,F为顶点的三角形与△CDA相似时,有两种情况:
①当∠CEF=90°时,如图1,△CEF∽△CDA,
∴$\frac{CE}{CD}=\frac{CF}{AC}$,
∵四边形ABCD为矩形,
∴∠D=90°,DC=AB=8,
由勾股定理得:AC=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∴FC=10-2t,
∴$\frac{t}{8}=\frac{10-2t}{10}$,
10t=80-16t,
t=$\frac{40}{13}$,
②当∠EFC=90°时,如图2,△CEF∽△CAD,
∴$\frac{CE}{AC}=\frac{CF}{CD}$,
∴$\frac{t}{10}=\frac{10-2t}{8}$,
8t=10(10-2t),
t=$\frac{25}{7}$,
∵t=10÷2=5,即0≤t≤5,
综上所述,当以C,E,F为顶点的三角形与△CDA相似时,t的值为$\frac{40}{13}$秒或$\frac{25}{7}$秒;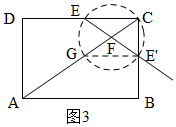
(2)当点E关于点F的对称点E′落在BC上时,如图3,则EF=E′F,
过E′作E′G∥AB,交AC于G,
∵DC∥AB,
∴E′G∥AB∥DC,
∴∠ECF=∠CGE′,
∵∠EFC=∠E′FG,
∴△EFC≌△E′FG,
∴FG=FC=10-2t,CE=E′G=t,
∴CG=2FC=20-4t,
∵E′G∥AB,
∴△CGE′∽△CAB,
∴$\frac{CG}{AC}=\frac{GE′}{AB}$,
∴$\frac{20-4t}{10}=\frac{t}{8}$,
t=$\frac{80}{21}$;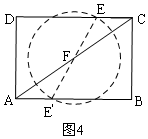
当点E关于点F的对称点E′落在AB上时,如图4,
同理得:△EFC≌△E′FA,
∴AF=FC,
∴2t=10-2t,
4t=10,
t=2.5,
∴当点E关于点F的对称点E′落在△ABC的内部(不包括边上)时,t的取值范围是2.5<t<$\frac{80}{21}$.
点评 本题考查了矩形的性质、全等三角形、相似三角形的性质和判定以及中心对称的性质,第1问采用了分类讨论的思想,注意不要漏解;第2问采用了数形结合的思想,要想求t的取值,求出点E′在两边上时的时间t,即可得出结论.


科目:初中数学 来源: 题型:选择题
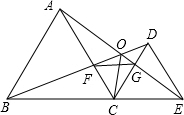 如图,已知△ABC和△DCE均是等边三角形,点B、C、E在同一条直线上,AE与BD交于点O,AE与CD交于点G,AC与BD交于点F,连接OC、FG,则下列结论:①AE=BD;②AO=BF;③FG∥BE;④∠BOC=∠EOC;⑤BO=OC+AO,其中正确的结论有( )个.
如图,已知△ABC和△DCE均是等边三角形,点B、C、E在同一条直线上,AE与BD交于点O,AE与CD交于点G,AC与BD交于点F,连接OC、FG,则下列结论:①AE=BD;②AO=BF;③FG∥BE;④∠BOC=∠EOC;⑤BO=OC+AO,其中正确的结论有( )个.| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
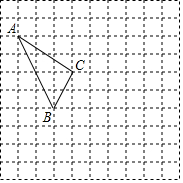 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).
在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com