
【题目】(教材回顾)
七上教材有这样一段文字:人们通过长期观察发现如果早晨天空中棉絮的高积云,那么午后常有雷雨降临,于是有了“朝有破絮云,午后雷雨临”的谚语.在数学的学习过程中,我们经常用这样的方法探究规律.
(数学问题)
四边形有4个顶点,如果在它的内部再画n个点,并以这(n+4)个点为顶点画三角形,那么最多可以剪得多少个这样的三角形?
(问题探究)
为了解决这个问题,我们可以从n=1,n=2,n=3等具体的、简单的情形入手,探索最多可以剪得的三角形个数的变化规律.
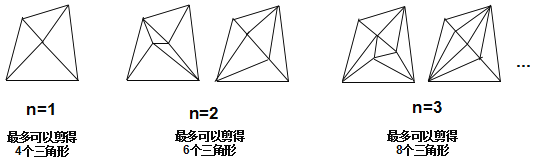
(问题解决)
(1)当四边形内有4个点时,最多剪得的三角形个数为______________;
(2)你发现的变化规律是:四边形内的点每增加1个,最多剪得的三角形增加______个;
(3)猜想:当四边形内点的个数为n时,最多可以剪得_______________个三角形;像这样通过对简单情形的观察、分析,从特殊到一般地探索这类现象的规律、提出猜想的思想方法称为归纳.
(问题拓展)
请你尝试用归纳的方法探索4+6+8+10+…+2n+(2n+2)的和是多少?
【答案】(1)10;(2)2;(3)2n+2;问题拓展:n2+3n.
【解析】
(1)根据【问题探究】提供的数据,进而得出答案;
(2)利用探究数据得出三角形个数的变化规律即可;
(3)因为6-4=8-6=2,所以四边形内的点每增加1个,最多可以剪得的三角形增加2个;∵四边形内点的个数为1时,最多剪出的小三角形个数4=2×1+2,因为四边形内点的个数为2时,最多剪出的小三角形个数6=2×2+2,四边形内点的个数为3时,最多剪出的小三角形个数8=2×3+2,所以四形内点的个数为n时,最多剪出的小三角形个数2n+2;
[问题拓展]列表归纳即可得到结论.
(1)∵当四边形内点的个数为1时,最多可以剪得4个三角形;
当四形内点的个数为2时,最多可以剪得6个三角形;
当四边形内点的个数为3时,最多可以剪得8个三角形;
当四边形内点的个数为4时,最多可以剪得10个三角形;
(2)利用(1)中变化规律得出:因为6-4=8-6=2,所以四边形内的点每增加1个,最多可以剪得的三角形增加2个;
(3)∵四边形内点的个数为1时,最多剪出的小三角形个数4=2×1+2,因为四边形内点的个数为2时,最多剪出的小三角形个数6=2×2+2,四边形内点的个数为3时,最多剪出的小三角形个数8=2×3+2,所以四形内点的个数为n时,最多剪出的小三角形个数2n+2;
[问题拓展]
列表归纳
加数的个数 | 和 |
4+6 | 22+2×3 |
4+6+8 | 32+3×3 |
4+6+8+10 | 42+4×3 |
… | … |
4+6+8+10+…+(2n+2) | n2+3n |
∴4+6+8+10+…+2n+(2n+2)= n2+3n


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
【题目】王华、张伟两位同学分别将自己10次数学自我检测的成绩绘制成如下统计图:
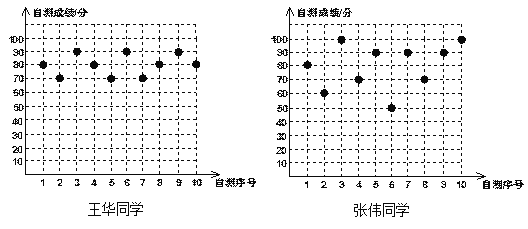
(1)根据上图中提供的数据列出如下统计表:
平均成绩(分) | 中位数(分) | 众数(分) | 方差(S2) | |
王华 | 80 | b | 80 | d |
张伟 | a | 85 | c | 260 |
则a= ,b= ,c= ,d= ,
(2)将90分以上(含90分)的成绩视为优秀,则优秀率高的是 .
(3)现在要从这两个同学选一位去参加数学竞赛,你可以根据以上的数据给老师哪些建议?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】世界卫生组织预计:到2025年,全世界将会有一半人面临用水危机,为了倡导“节约用水,从我做起”,某县政府决定对县直属机关300户家庭一年的月平均用水量进行调查,调查小组抽查了部分家庭月平均用水量(单位:吨),绘制条形图和扇形图如图所示.
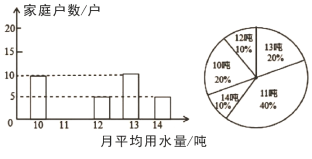
(1)请将条形统计图补充完整;
(2)这些家庭月平均用水量数据的平均数是_______,众数是______,中位数是_______;
(3)根据样本数据,估计该县直属机关300户家庭的月平均用水量不超过12吨的约有多少户.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用小立方块搭一个几何体,使它从正面和上面看到的形状如图所示,从上面看到形状中小正方形中的字母表示在该位置上小立方块的个数,请问:
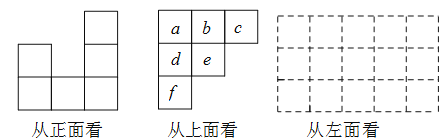
(1)![]() ,
,![]() 各表示几? 答:
各表示几? 答:![]() _____ ,
_____ ,![]() _____;
_____;
(2)这个几何体最少由_____个小立方块搭成,最多由____个小立方块搭成;
(3)能搭出满足条件的几何体共有____种情况,其中从左面看这个几何体的形状图共有____种,请在所给网格图中画出其中的任意一种.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,在△ABC中,∠B=40°,∠C=80°,AD⊥BC于D,且AE平分∠BAC,求∠EAD的度数.
(2)上题中若∠B=40°,∠C=80°改为∠C>∠B,其他条件不变,请你求出∠EAD与∠B、∠C之间的数列关系?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=![]() ;⑤S四边形CDEF=
;⑤S四边形CDEF=![]() S△ABF,其中正确的结论有( )
S△ABF,其中正确的结论有( )
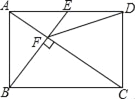
A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,AC=60 cm,∠A=60°,点D从点C出发沿CA方向以4 cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2 cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由;
(3)当t为何值时,△DEF为直角三角形?请直接写出结果;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K﹣∠H=27°,则∠K=( )
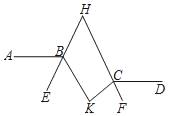
A. 76° B. 78° C. 80° D. 82°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习“利用三角函数测高”后,某综合实践活动小组实地测量了凤凰山与中心广场的相对高度AB,其测量步骤如下:
(1)在中心广场测点C处安置测倾器,测得此时山顶A的仰角∠AFH=30°;
(2)在测点C与山脚B之间的D处安置测倾器(C、D与B在同一直线上,且C、D之间的距离可以直接测得),测得此时山顶上红军亭顶部E的仰角∠EGH=45°;
(3)测得测倾器的高度CF=DG=1.5米,并测得CD之间的距离为288米;
已知红军亭高度为12米,请根据测量数据求出凤凰山与中心广场的相对高度AB.(![]() 取1.732,结果保留整数)
取1.732,结果保留整数)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com