
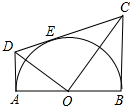
 如图,AB为半圆O的直径,CD切⊙O于点E,AD、BC分别切⊙O于A、B两点,AD与CD相交于D,BC与CD相交于C,连接OD、OC,对于下列结论:①OD2=DE•CD;②AD+BC=CD;③OD=OC;④S梯形ABCD=CD•OA;⑤∠DOC=90°;⑥若切点E在半圆上运动(A、B两点除外),则线段AD与BC的积为定值.其中正确的个数是( )
如图,AB为半圆O的直径,CD切⊙O于点E,AD、BC分别切⊙O于A、B两点,AD与CD相交于D,BC与CD相交于C,连接OD、OC,对于下列结论:①OD2=DE•CD;②AD+BC=CD;③OD=OC;④S梯形ABCD=CD•OA;⑤∠DOC=90°;⑥若切点E在半圆上运动(A、B两点除外),则线段AD与BC的积为定值.其中正确的个数是( )| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
分析 根据切线的性质得到三个角为直角,且利用切线长定理得到DE=DA,CE=CB,由CD=DE+EC,等量代换可得出CD=AD+BC,选项②正确;由AD=ED,OD为公共边,根据全等三角形的性质得到∠AOD=∠EOD,同理得到∠EOC=∠BOC,而这四个角之和为平角,可得出∠DOC为直角,选项①正确;根据相似三角形的性质得比例可得出OD2=DE•CD,选项⑤正确;由△ODE∽△OEC,$\frac{OD}{OC}=\frac{DE}{OE}$,得到OD≠OC,选项③错误;根据射影定理即可得到AD•BC=OE2,于是得到线段AD与BC的积为定值,故⑥正确.
解答 解:连接OE,如图所示:
∵AD与圆O相切,DC与圆O相切,BC与圆O相切,
∴∠DAO=∠DEO=∠OBC=90°,
∴DA=DE,CE=CB,AD∥BC,
∴CD=DE+EC=AD+BC,选项②正确;
∴S梯形ABCD=$\frac{1}{2}$(AD+BC)•AB=CD•OA;选项④正确;
在Rt△ADO和Rt△EDO中,
$\left\{\begin{array}{l}{OD=OD}\\{DA=DE}\end{array}\right.$,
∴Rt△ADO≌Rt△EDO(HL),
∴∠AOD=∠EOD,
同理Rt△CEO≌Rt△CBO,
∴∠EOC=∠BOC,
又∵∠AOD+∠DOE+∠EOC+∠COB=180°,
∴2(∠DOE+∠EOC)=180°,即∠DOC=90°,选项⑤正确;
∴∠DOC=∠DEO=90°,又∠EDO=∠ODC,
∴△EDO∽△ODC,
∴$\frac{OD}{CD}$=$\frac{DE}{OD}$,即OD2=DC•DE,选项①正确;
同理△ODE∽△OEC,
∴$\frac{OD}{OC}=\frac{DE}{OE}$,
∴OD≠OC,选项③错误;
∵∠COD=90°,OE⊥CD,
∴OE2=CE•DE,
∵DA=DE,CE=CB,
∴AD•BC=OE2,
∴线段AD与BC的积为定值,故⑥正确.
故选A.
点评 此题考查了切线的性质,切线长定理,相似三角形的判定与性质,全等三角形的判定与性质,利用了转化的数学思想,熟练掌握定理及性质是解本题的关键.


科目:初中数学 来源: 题型:填空题
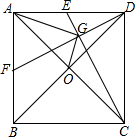 已知如图,正方形ABCD的对角线AC、BD交于O,点E、F分别是AD、AB边的中点,连接DF、CE交于点G,连接AG、OG.若AD=2,则OG=$\frac{\sqrt{10}}{5}$.
已知如图,正方形ABCD的对角线AC、BD交于O,点E、F分别是AD、AB边的中点,连接DF、CE交于点G,连接AG、OG.若AD=2,则OG=$\frac{\sqrt{10}}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k>0,b>0 | B. | k>0,b<0 | C. | k<0,b>0 | D. | k<0,b<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,抛物线y=mx2-2mx+m-4(m≠0)的顶点为A,与x轴交于B,C两点(点B在点C左侧),与y轴交于点D.
在平面直角坐标系xOy中,抛物线y=mx2-2mx+m-4(m≠0)的顶点为A,与x轴交于B,C两点(点B在点C左侧),与y轴交于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB为⊙O的直径,AB=2,点在M在QO上,MC垂直平分OA,点N为直线AB上一动点(N不与A重合),若△MNP∽△MAC,PC与直线AB所夹锐角为α.
如图,AB为⊙O的直径,AB=2,点在M在QO上,MC垂直平分OA,点N为直线AB上一动点(N不与A重合),若△MNP∽△MAC,PC与直线AB所夹锐角为α.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,直线l上所有点的坐标都是方程x+y=2的解,直线m上所有点的坐标都是方程x-y=0的解.观察该图回答:直线l与m的交点M的坐标为(1,1).方程组$\left\{\begin{array}{l}{x+y=2}\\{x-y=0}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$.
如图,直线l上所有点的坐标都是方程x+y=2的解,直线m上所有点的坐标都是方程x-y=0的解.观察该图回答:直线l与m的交点M的坐标为(1,1).方程组$\left\{\begin{array}{l}{x+y=2}\\{x-y=0}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
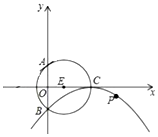 如图,⊙E的圆心E(3,0),半径为5,⊙E与y轴相交于A、B两点(点A在点B的上方),与x轴的正半轴交于点C,直线l的解析式为y=kx+4k+1(k为实数),以点C为顶点的抛物线过点B.
如图,⊙E的圆心E(3,0),半径为5,⊙E与y轴相交于A、B两点(点A在点B的上方),与x轴的正半轴交于点C,直线l的解析式为y=kx+4k+1(k为实数),以点C为顶点的抛物线过点B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com