
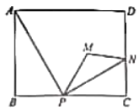
【题目】如图,在矩形ABCD中,已知![]() ,
,![]() ,点P是边BC上一动点(点P不与点B,C重合),连接AP,作点B关于直线AP的对称点M,连接MP,作
,点P是边BC上一动点(点P不与点B,C重合),连接AP,作点B关于直线AP的对称点M,连接MP,作![]() 的角平分线交边CD于点N.则线段MN的最小值为_______________
的角平分线交边CD于点N.则线段MN的最小值为_______________
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知锐角∠AOB如图,(1)在射线OA上取一点C,以点O为圆心,OC长为半径作![]() ,交射线OB于点D,连接CD;
,交射线OB于点D,连接CD;
(2)分别以点C,D为圆心,CD长为半径作弧,交![]() 于点M,N;
于点M,N;
(3)连接OM,MN.
根据以上作图过程及所作图形,下列结论中错误的是( )

A. ∠COM=∠CODB. 若OM=MN,则∠AOB=20°
C. MN∥CDD. MN=3CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店计划采购甲、乙两种不同型号的平板电脑共20台,已知甲型平板电脑进价1600元,售价2000元;乙型平板电脑进价为2500元,售价3000元.
(1)设该商店购进甲型平板电脑x台,请写出全部售出后该商店获利y与x之间函数表达式.
(2)若该商店采购两种平板电脑的总费用不超过39200元,全部售出所获利润不低于8500元,请设计出所有采购方案,并求出使商店获得最大利润的采购方案及最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】病毒虽无情,人间有大爱.2020年,在湖北省抗击新冠病毒的战“疫”中,全国(除湖北省外)共有30个省(区、市)及军队的医务人员在党中央全面部署下,白衣执甲,前赴后继支援湖北省.全国30个省(区、市)各派出支援武汉的医务人员频数分布直方图(不完整)和扇形统计图如下:(数据分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .)
.)
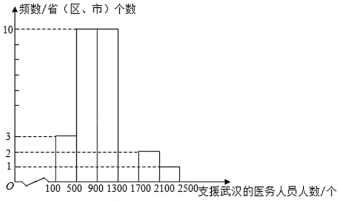
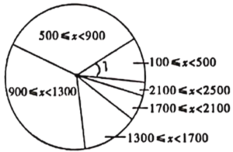
根据以上信息回答问题:
(1)补全频数分布直方图.
(2)求扇形统计图中派出人数大于等于100小于500所占圆心角度数.
据新华网报道在支援湖北省的医务人员大军中,有“90后”也有“00后”,他们是青春的力量,时代的脊梁.小华在收集支援湖北省抗疫宣传资料时得到这样一组有关“90后”医务人员的数据:
![]() 市派出的1614名医护人员中有404人是“90后”;
市派出的1614名医护人员中有404人是“90后”;
![]() 市派出的338名医护人员中有103人是“90后”;
市派出的338名医护人员中有103人是“90后”;
![]() 市某医院派出的148名医护人员中有83人是“90后”.
市某医院派出的148名医护人员中有83人是“90后”.
(3)请你根据小华得到的这些数据估计在支援湖北省的全体医务人员(按4.2万人计)中,“90后”大约有多少万人?(写出计算过程,结果精确到0.1万人)
查看答案和解析>>
科目:初中数学 来源: 题型:
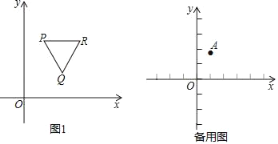
【题目】在平面直角坐标系XOY中,点P的坐标为(x1,y1),点Q的坐标为(x2,y2),且x1≠x2,若P、Q为某等边三角形的两个顶点,且有一边与x轴平行(含重合),则称P、Q互为“向善点”.如图1为点P、Q互为“向善点”的示意图.已知点A的坐标为(1,![]() ),点B的坐标为(m,0)
),点B的坐标为(m,0)
(1)在点M(﹣1,0)、S(2,0)、T(3,3![]() )中,与A点互为“向善点”的是_____;
)中,与A点互为“向善点”的是_____;
(2)若A、B互为“向善点”,求直线AB的解析式;
(3)⊙B的半径为![]() ,若⊙B上有三个点与点A互为“向善点”,请直接写出m的取值范围.
,若⊙B上有三个点与点A互为“向善点”,请直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
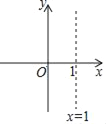
【题目】在平面直角坐标系中,抛物线y=x2﹣2x+c(c为常数)的对称轴如图所示,且抛物线过点C(0,c).
(1)当c=﹣3时,点(x1,y1)在抛物线y=x2﹣2x+c上,求y1的最小值;
(2)若抛物线与x轴有两个交点,自左向右分别为点A、B,且OA=![]() OB,求抛物线的解析式;
OB,求抛物线的解析式;
(3)当﹣1<x<0时,抛物线与x轴有且只有一个公共点,求c的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校运动会的立定跳远和30秒跳绳两个单项比赛分成预赛和决赛两个阶段,下表为10名学生的预赛成绩,其中有三个数据模糊.
学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
跳远(米) | 1.96 | 1.92 | 1.82 | 1.80 | 1.78 | 1.76 | 1.74 | 1.72 | 1.68 | 1.60 |
跳绳(次) | 63 |
| 75 | 60 | 63 | 72 | 70 |
|
| 65 |
在这10名学生中,进入立定跳远决赛的有8人,同时进入立定跳远决赛和30秒跳绳决赛的有6人,则( )
A.5号学生进入30秒跳绳决赛
B.2号学生进入30秒跳绳决赛
C.8号学生进入30秒跳绳决赛
D.9号学生进入30秒跳绳决赛
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com