
【题目】小明在一次数学兴趣小组活动中,进行了如下探索活动.
问题原型:如图(1),在矩形ABCD中,AB=6,AD=8,P、Q分别是AB、AD边的中点,以AP、AQ为邻边作矩形APEQ,连接CE,则CE的长为 (直接填空)
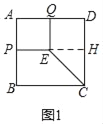
问题变式:(1)如图(2),小明让矩形APEQ绕着点A逆时针旋转至点E恰好落在AD上,连接CE、DQ,请帮助小明求出CE和DQ的长,并求DQ:CE的值.
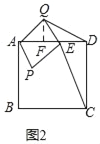
(2)如图(3),当矩形APEQ绕着点A逆时针旋转至如图(3)位置时,请帮助小明判断DQ:CE的值是否发生变化?若不变,说明理由.若改变,求出新的比值.
问题拓展:若将“问题原型”中的矩形ABCD改变为平行四边形ABCD,且AB=3![]() ,AD=7,∠B=45°,P、Q分别是AB、AD边上的点,且AP=
,AD=7,∠B=45°,P、Q分别是AB、AD边上的点,且AP=![]() AB,AQ=
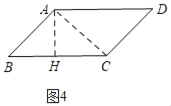
AB,AQ=![]() AD,以AP、AQ为邻边作平行四边形APEQ.当平行四边形APEQ绕着点A逆时针旋转至如图(4)位置时,连接CE、DQ.请帮助小明求出DQ:CE的值.
AD,以AP、AQ为邻边作平行四边形APEQ.当平行四边形APEQ绕着点A逆时针旋转至如图(4)位置时,连接CE、DQ.请帮助小明求出DQ:CE的值.

【答案】问题原型:(1)CE=5;问题变式:(1)CE=3![]() ,DQ=
,DQ=![]() ,DQ:CE=4:5;(2)不变,见解析;问题拓展:
,DQ:CE=4:5;(2)不变,见解析;问题拓展:![]() =
=![]()
【解析】
问题原型:如图1中,延长PE交CD于H,则四边形QEHD是矩形.在Rt△CEH中,利用勾股定理即可解决问题;
问题变式:(1)如图2中,作FQ⊥AD于F.利用勾股定理相似三角形的性质,分别求出CE、DQ即可解决问题;
(2)不变.理由如下:连接AE、AC.只要证明△ACE∽△ADQ,列比例式即可解决问题;
问题拓展:在图4中,计算AC的长,同理得△ACE∽△ADQ,通过计算即可解决问题.
问题原型:
如图1中,延长PE交CD于H,则四边形QEHD是矩形,
在Rt△CEH中,EH=DQ=4,CH=PB=AP=3,
∴CE=![]() =5,
=5,
故答案为:5;
问题变式:
(1)如图2中,过Q作QF⊥AD于F,
在矩形APEQ中,∵AP=3,EP=4,
∴AE=5,ED=8﹣5=3,
在Rt△CED中,CE=![]() =3
=3![]() ,
,
∵∠QAF=∠QAE,∠AFQ=∠AQE=90°,
∴△AQF∽△AEQ,
∴![]() ,
,
∴![]() ,
,
∴FQ=![]() ,
,
∴AF=![]() ,
,
∴DF=8﹣![]() =
=![]() ,
,
由勾股定理得:DQ=![]() ,
,
∴DQ:CE=![]() :3
:3![]() =4:5;
=4:5;
(2)不变,理由如下:连接AE、AC,
由旋转可知:∠QAD=∠EAC,
由勾股定理可知:AC=10,AE=5,
∴![]() ,
,![]() ,
,
∴![]()
![]() ,
,
∴△ACE∽△ADQ,
∴![]() ;
;
问题拓展:如图4中,过A作AH⊥BC于H,连接AC,
∵∠B=45°,
∴△ABH是等腰直角三角形,
∵AB=3![]() ,
,
∴AH=BH=3
∴CH=7﹣3=4,
由勾股定理得:AC=![]() =5,
=5,
∴![]() ,
,
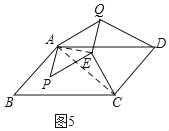
如图5,连接AE、AC,
同理APEQ中,AP=![]() ,PE=
,PE=![]() ,得AE=
,得AE=![]() ,
,
∴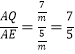 ,
,
由旋转得:∠QAD=∠EAC,
∴△ACE∽△ADQ,可得:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,从热气球C处测得地面A,B两点的俯角分别是30°、45°,如果此时热气球C处的高度CD为100米,点A,D,B在同一直线上,则AB两点的距离是( )
A.200米
B.200 ![]() 米
米
C.220 ![]() 米
米
D.100( ![]() )米
)米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知:点A(0,0),B( ![]() ,0),C(0,1)在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1 , 第2个△B1A2B2 , 第3个△B2A3B3 , …,则第n个等边三角形的边长等于 .
,0),C(0,1)在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1 , 第2个△B1A2B2 , 第3个△B2A3B3 , …,则第n个等边三角形的边长等于 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数 ![]() 的图象经过点(
的图象经过点( ![]() ,8),直线y=﹣x+b经过该反比例函数图象上的点Q(4,m).
,8),直线y=﹣x+b经过该反比例函数图象上的点Q(4,m).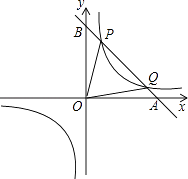
(1)求上述反比例函数和直线的函数表达式;
(2)设该直线与x轴、y轴分别相交于A、B两点,与反比例函数图象的另一个交点为P,连接0P、OQ,求△OPQ的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,F是BC上的一点,直线DF与AB的延长线相交于点E,BP∥DF,且与AD相交于点P,则图中相似三角形的组数为( )
A.3
B.4
C.5
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)请在横线上填写合适的内容,完成下面的证明:
如图①如果AB∥CD,求证:∠APC=∠A+∠C.
证明:过P作PM∥AB.
所以∠A=∠APM,( )
因为PM∥AB,AB∥CD(已知)
所以∠C= ( )
因为∠APC=∠APM+∠CPM
所以∠APC=∠A+∠C(等量代换)
(2)如图②,AB∥CD,根据上面的推理方法,直接写出∠A+∠P+∠Q+∠C= .
(3)如图③,AB∥CD,若∠ABP=x,∠BPQ=y,∠PQC=z,∠QCD=m,则m= (用x、y、z表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠ABC=70°,以B为圆心,任意长为半径画弧交AB,BC于点E,F,再分别以点E,F为圆心、以大于![]() EF长为半径画弧,两弧交于点P,作射线BP交AC于点D,则∠BDC为( )度.
EF长为半径画弧,两弧交于点P,作射线BP交AC于点D,则∠BDC为( )度.
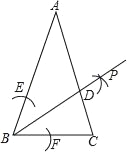
A. 65 B. 75 C. 80 D. 85
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①, 已知△ABC中, ∠BAC=90°, AB=AC, AE是过A的一条直线, 且B、C在AE的异侧, BD⊥AE于D, CE⊥AE于E.

(1)求证: BD=DE+CE.
(2)若直线AE绕A点旋转到图②位置时(BD<CE), 其余条件不变, 问BD与DE、CE的数量关系如何? 请给予证明;
(3)若直线AE绕A点旋转到图③位置时(BD>CE), 其余条件不变, 问BD与DE、CE的数量关系如何? 请直接写出结果, 不需证明.
(4)根据以上的讨论,请用简洁的语言表达BD与DE,CE的数量关系。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com