
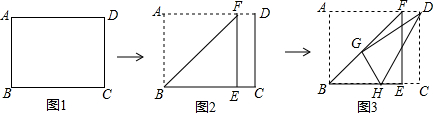
分析 过G点作MN∥AB,交AD、BC于点M、N,可知四边形ABEF为正方形,可求得AF的长,可判断①,且△BNG和△FMG为等腰三角形,设BN=x,则可表示出GN、MG、MD,利用折叠的性质可得到CD=DG,在Rt△MDG中,利用勾股定理可求得x,再利用△MGD∽△NHG,可求得NH、GH和HC,则可求得BH,容易判断②③④,可得出答案.
解答 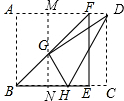 解:如图,过点G作MN∥AB,分别交AD、BC于点M、N,
解:如图,过点G作MN∥AB,分别交AD、BC于点M、N,
∵四边形ABCD为矩形,
∴AB=CD=10,BC=AD=12,
由折叠可得AB=BE,且∠A=∠ABE=∠BEF=90°,
∴四边形ABEF为正方形,
∴AF=AB=10,
故①正确;
∵MN∥AB,
∴△BNG和△FMG为等腰直角三角形,且MN=AB=10,
设BN=x,则GN=AM=x,MG=MN-GN=10-x,MD=AD-AM=12-x,
又由折叠的可知DG=DC=10,
在Rt△MDG中,由勾股定理可得MD2+MG2=GD2,
即(12-x)2+(10-x)2=102,解得x=4,
∴GN=BN=4,MG=6,MD=8,
又∠DGH=∠C=∠GMD=90°,
∴∠NGH+∠MGD=∠MGD+∠MDG=90°,
∴∠NGH=∠MDG,且∠DMG=∠GNH,
∴△MGD∽△NHG,
∴$\frac{MD}{GN}$=$\frac{MG}{NH}$=$\frac{DG}{GH}$,即$\frac{8}{4}$=$\frac{6}{NH}$=$\frac{10}{GH}$,
∴NH=3,GH=CH=5,
∴BH=BC-HC=12-5=7,
故④正确;
又△BNG和△FMG为等腰直角三角形,且BN=4,MG=6,
∴BG=4$\sqrt{2}$,GF=6$\sqrt{2}$,
∴△BGF的周长=BG+GH+BH=4$\sqrt{2}$+5+7=12+4$\sqrt{2}$,$\frac{BG}{GF}$=$\frac{4\sqrt{2}}{6\sqrt{2}}$=$\frac{2}{3}$,
故②不正确;③正确;
综上可知正确的为①③④,
故答案为:①③④.
点评 本题为四边形的综合应用,涉及知识点有矩形的性质、正方形的判定和性质、等腰直角三角形的性质、相似三角形的判定和性质、折叠的性质及方程思想等.过G点作AB的平行线,构造等腰直角三角形,利用方程思想在Rt△GMD中得到方程,求得BN的长度是解题的关键.本题考查知识点较多,综合性质较强,难度较大.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:解答题
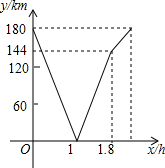 一辆货车从A地去B地,一辆轿车从B地去A地,同时出发,匀速行驶,各自到达终点后停止,轿车的速度大于货车的速度.两辆车之间的距离为y(km)与货车行驶的时间为x(h)之间的函数关系如图所示.
一辆货车从A地去B地,一辆轿车从B地去A地,同时出发,匀速行驶,各自到达终点后停止,轿车的速度大于货车的速度.两辆车之间的距离为y(km)与货车行驶的时间为x(h)之间的函数关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
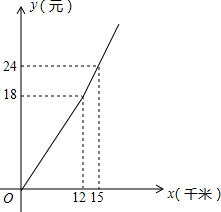 随着“互联网+”时代的到来,一种新型的打车方式受到大众欢迎.该打车方式采用阶梯收费标准.打车费用y(单位:元)与行驶里程x(单位:千米)的函数关系如图所示.如果小明某次打车行驶里程为20千米,则他的打车费用为( )
随着“互联网+”时代的到来,一种新型的打车方式受到大众欢迎.该打车方式采用阶梯收费标准.打车费用y(单位:元)与行驶里程x(单位:千米)的函数关系如图所示.如果小明某次打车行驶里程为20千米,则他的打车费用为( )| A. | 32元 | B. | 34元 | C. | 36元 | D. | 40元 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
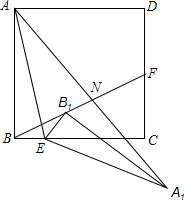 如图,正方形ABCD中,AB=4,点E是BC上靠近点B的四等分点,点F是CD的中点,连接AE、BF将△ABE着点E按顺时针方向旋转,使点B落在BF上的B1处位置处,点A经过旋转落在点A1位置处,连接AA1交BF于点N,则AN的长为$\frac{2\sqrt{85}}{5}$.
如图,正方形ABCD中,AB=4,点E是BC上靠近点B的四等分点,点F是CD的中点,连接AE、BF将△ABE着点E按顺时针方向旋转,使点B落在BF上的B1处位置处,点A经过旋转落在点A1位置处,连接AA1交BF于点N,则AN的长为$\frac{2\sqrt{85}}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com