
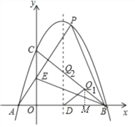
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣1,0),B(4,0),与y轴交于点C(0,4).
(1)求此抛物线的解析式;
(2)设点P(2,n)在此抛物线上,AP交y轴于点E,连接BE,BP,请判断△BEP的形状,并说明理由;
(3)设抛物线的对称轴交x轴于点D,在线段BC上是否存在点Q,使得△DBQ成为等腰直角三角形?若存在,求出点Q的坐标;若不存在,说明理由.

【答案】(1)y=﹣x2+3x+4;(2)△BEP为等腰直角三角形,理由见解析;(3)存在,Q的坐标为![]() 或
或![]() .
.
【解析】试题分析:(1)待定系数法求二次函数解析式.(2)先求出直线AP解析式,分别求出BE,EP,BP的长度,由勾股定理逆定理△BEP的形状.(3)先求出二次函数的顶点,分类讨论,若BQ=DQ,BQ1⊥DQ1,∠BDQ=45°,过点Q1作Q1M⊥OB,垂足为M,可求得△DBQ是等腰三角形,可以得到Q点,若DQ2=BD,DQ2⊥BD,可以计算出Q点.
试题解析:
解:(1)∵抛物线上A、B、C三点坐标代入抛物线解析式y=ax2+bx+c
得,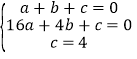 ,
,
解得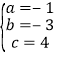 ,
,
∴抛物线的解析式为y=﹣x2+3x+4.
(2)结论:△BEP为等腰直角三角形,理由如下:
∵点P(2,n)在此抛物线上,
∴n=﹣4+6+4=6,
∴P点坐标为(2,6).
设直线AP解析式为y=kx+b,
把A、P两点坐标代入可得![]() ,
,
解得![]() ,
,
∴直线AP的解析式为y=2x+2,
令x=0可得y=2,则E点坐标为(0,2).
∵B(4,0),P(2,6),
∴BP=2![]() ,BE=2
,BE=2![]() ,EP=2
,EP=2![]()
∴BE2+EP2=20+20=40=BP2,且BE=EP,
∴△BEP为等腰直角三角形.
(3)存在.
∵y=﹣x2+3x+4=﹣(x﹣![]() )2+
)2+![]() ,
,
∴顶点的坐标为(![]() ,
,![]() ),
),
∵OB=OC=4,∴BC=4![]() ,∠ABC=45°.
,∠ABC=45°.
以下分两种情况:
①若BQ=DQ,BQ1⊥DQ1,∠BDQ=45°,如图,过点Q1作Q1M⊥OB,垂足为M,
∵BQ1=DQ1,BD=4﹣![]() =
=![]() ,
,
∴BM=Q1![]() ,OM=4﹣
,OM=4﹣![]() =
=![]() ,
,
∴Q1的坐标为Q1(![]() ,
,![]() ).
).
②若DQ2=BD=![]() ,DQ2⊥BD,易得BC所在的直线解析式为y=﹣x+4,
,DQ2⊥BD,易得BC所在的直线解析式为y=﹣x+4,
代入x=![]() ,得y=﹣
,得y=﹣![]() +4=
+4=![]() ,
,
∴DQ2=BD=![]() ,∴△BDQ2是等腰直角三角形,
,∴△BDQ2是等腰直角三角形,
所以Q2的坐标为Q2(![]() ,
,![]() ),
),
综上所述,Q的坐标为Q1(![]() ,
,![]() )或Q2(
)或Q2(![]() ,
,![]() ).
).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,一枚运载火箭从距雷达站C处5km的地面O处发射,当火箭到达点A,B时,在雷达站C处测得点A,B的仰角分别为34°,45°,其中点O,A,B在同一条直线上.求A,B两点间的距离(结果精确到0.1km).
(参考数据:sin34°=0.56,cos34°=0.83,tan34°=0.67.)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠B=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于点E.

(1)若∠BDA=115°,则∠BAD= °,∠DEC= °;
(2)若DC=AB,求证:△ABD≌△DCE;
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数;若不可以,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年3月12日是第41个植树节,某单位积极开展植树活动,决定购买甲、乙两种树苗,用800元购买甲种树苗的棵数与用680元购买乙种树苗的棵数相同,乙种树苗每棵比甲种树苗每棵少6元.
(1)求甲种树苗每棵多少元?
(2)若准备用3800元购买甲、乙两种树苗共100棵,则至少要购买乙种树苗多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两种商品原来的单价和为100元.因市场变化,甲商品降价10%,乙商品提价40%,调价后两种商品的单价和比原来的单价和提高了20%.甲、乙两种商品原来的单价各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】烟台享有“苹果之乡”的美誉.甲、乙两超市分别用3000元以相同的进价购进质量相同的苹果.甲超市销售方案是:将苹果按大小分类包装销售,其中大苹果400千克,以进价的2倍价格销售,剩下的小苹果以高于进价10%销售.乙超市的销售方案是:不将苹果按大小分类,直接包装销售,价格按甲超市大、小两种苹果售价的平均数定价.若两超市将苹果全部售完,其中甲超市获利2100元(其它成本不计).问:
(1)苹果进价为每千克多少元?
(2)乙超市获利多少元?并比较哪种销售方式更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,
D为AB边上一点.
(1)求证:△ACE≌△BCD
(2)若AD=6,BD=8,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班级45名同学自发筹集到1700元资金,用于初中毕业时各项活动的经费,计划将资金用于给每名同学购买一件文化衫或一本制作精美的相册作为纪念品,已知每件文化衫28元,每本相册20元.
设购买的文化衫件数为x(x为非负整数).
(Ⅰ)根据题意,填写下表:
购买的文化衫件数(件) | 5 | 10 | 20 | 30 | … |
买文化衫所学费用(元) | 140 |
| 560 |
| … |
买相册所需费用(元) | 800 |
| 500 |
| … |
(Ⅱ)设购买文化衫和相册所需费用共W元,求W与购买的文化衫件数x的函数关系式;
(Ⅲ)通过商议,决定拿出不少于540元旦不超过570元的资金用于请专业人士牌照,其余则用于购买文化衫和相册,购买文化衫和相册有哪几种方案?为使拍照的资金更充足,应选择哪种方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1:y1=2x+1与坐标轴交于A,C两点,直线l2: y2=-x-2与坐标轴交于B,D两点,两直线交于P点.

(1)求P点的坐标;
(2)求△APB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com